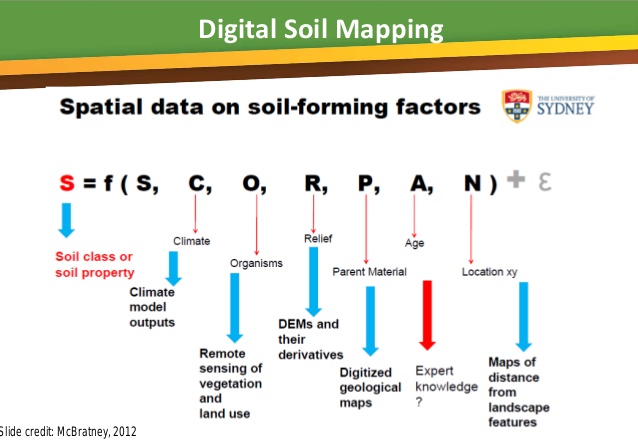
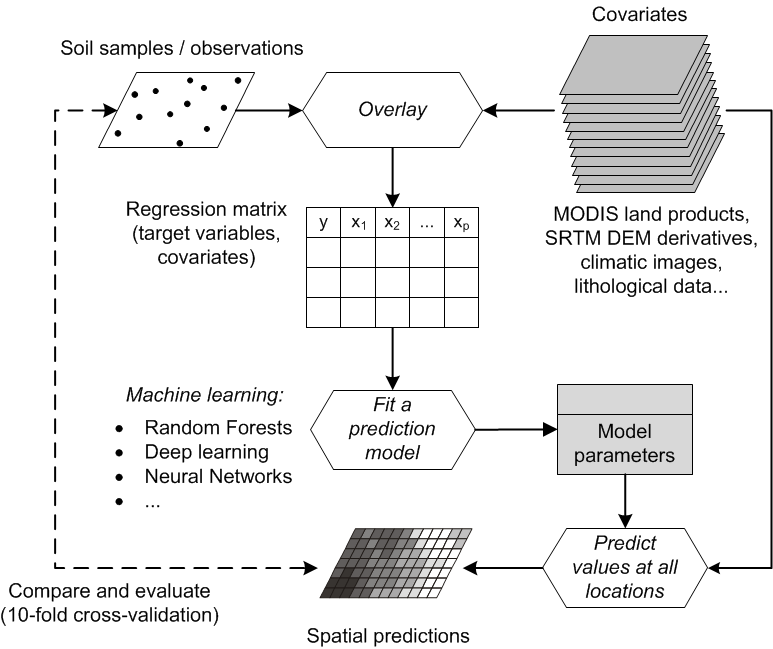
12 Digital (Soil) Mapping
Tobler’s Low of Geography (1970):
\(\quad\) “Everything is related to everything else, but near things are more related than distant things”.
12.1 Useful links
- Introduction to visualising spatial data in R
- Spatial Data Science with R and “terra”
- Spatial data in R: Using R as a GIS
- See the book Intro to GIS and Spatial Analysis by Manuel Gimond
- See the tutorial Spatial analysis > Interpolation within the digital resource Spatial Data Science with R and “terra”
12.4 Methods or Estimators
Outline the distinction between deterministic and statistical approaches.
See the book Intro to GIS and Spatial Analysis by Manuel Gimond:
- Deterministic approaches:
- proximity interpolation (aka Thiessen) (see my notes in live_exercise.R, PLF-2021) (draw an example and introduce the bisector)
- inverse distance weighted
- Statistical approaches:
- surface trend
- kriging
See THIS resource for an introductory list of models of spatial interpolation presented in the course:
- NULL model (average of all observations)
- Proximity polygons (nearest neighbour)
- Nearest neighbours (multiple neighbours)
- Inverse Distance Weighted (IDW)
- Linear Model (MLR: Multi-Linear Regression)
- Kriging
12.4.1 Common framework
The spatial interpolation of value \(\hat{z}({\mathbf u})\) at an unknown geospatial location \(\left({\mathbf u}\right)\) is given by the linear combination \(\left(\sum_{\alpha=1}^{n({\mathbf u})} \lambda_{\alpha}\right)\) of measured values \(\left(z({\mathbf u}_{\alpha})\right)\) in the neighbourhood of the unknown point \(\left({\mathbf u}\right)\).
The general formula used in this course is the following:
\(\hat{z}({\mathbf u}) = \displaystyle\sum_{\alpha=1}^{n({\mathbf u})} \lambda_{\alpha}({\mathbf u}) z({\mathbf u}_{\alpha})\)
where the weights must sum up to one:
\(\sum_{\alpha=1}^{n({\mathbf u})} \lambda_{\alpha}({\mathbf u}) = 1\)
Each method of spatial interpolation uses a distict criteria to assign weights \(\lambda_{\alpha}({\mathbf u})\) to neighbour measurement locations \({\mathbf u}_{\alpha}\).
In the following chapters more details about each spatial interpolation method are provided.