Skip to main content

A Minimal Set of Lectures Notes

23 Exercises

23.1 Vector Geodata

23.1.1 Upper Secondary School

Objective: create a Simple Feature object in R to manage and represent (the position and other attributes of) your upper secondary school.
Folder: ‘didattica/assignments/vector_ex01/’

Use Google Maps to get the coordinates of your school and populate the following attributes:

  • geometry: POINT XY (2D)
  • CRS: 4326 (as used in Google)
  • attributes:
    • ‘Name’
    • ‘Surname’
    • ‘SchoolName’
    • ‘GraduationDate’

Note: do not change the labels used for the attributes, including lowercase / uppercase characters.

Deliver the file named name_surname_school.geojson in the folder ‘didattica/assignments/vector_ex01/’.
[E.g. giuliano_langella_school.geojson]

Once all students complete the previous step, in folder vector_ex01 there will be more files. Each student has to import in R all the files and create a unique SF object in R fusing all the vector data from all students.

23.1.2 Agraria Teaching Rooms

Objective: create a map with all Points of Interest (PoI) of the Dep. of Agriculture in Portici.
Folder: ‘didattica/assignments/vector_ex02/’
Source: Aule lezioni e aule studio

Note: do not change the labels used for the attributes, including lowercase / uppercase characters.

23.1.2.1 Instructions

  1. Each student select one or more PoIs within the Department (select different PoIs)
  2. Go to geojson.io and draw a point on the map where you want to create a PoI
  3. Add the following attributes (take care of the UPPERCASE / lowercase letters):
    • ‘Aula’ → e.g. 1
    • ‘Ubicazione’ → e.g. Mascabruno
    • ‘Piano’ → e.g. Terra
    • ‘Posti’ → e.g. 200
    • ‘Descrizione’. → e.g. TAL
  4. Export from geojson.io using format GeoJSON.
  5. Load in RStudio Server file system
  6. Import in R as Simple Feature
  7. Create a plot / map to visualize the PoIs
  8. Export the simple feature using filename such as name_surname_poistudent.geojson (e.g. giuliano_langella_poistudent.geojson) in the shared folder ’didattica/assignments/vector_ex02/
  9. Wait that all students save their file
  10. Load in R all the files and create a unique SF object in R fusing all the PoIs from all students
  11. Save the SF object with all PoIs as name_surname_poiagraria.geojson (e.g. giuliano_langella_poiagraria.geojson)

23.1.3 Alberi monumentali

Objective: Create a simple feature of monumental trees in Italy.
Folder: ‘didattica/assignments/vector_ex03/’

    1. Creare un geodato vettoriale in RStudio – per catalogare alberi monumentali – con le seguenti specifiche:
      • tipo di geometria: punto
      • reperire la posizione di un albero monumentale o di un bosco su Google Maps (esso usa coordinate geografiche nel sistema di riferimento WGS84, caratterizzato da codice EPSG:4326)
      • step 01: creare un oggetto di classe sfg (Simple Feature Geometry)
      • step 02: creare un oggetto di class sfc (Simple Feature Column), ricordandoci che le coordinate sono soltanto dei numeri…(quindi cosa manca?)
      • step 03: aggiungere al “dove” il “cosa”, ovvero aggiungere le seguenti informazione nella tabella degli attributi:
        • campo “age” di tipo numerico, per indicare il numero di anni
        • campo “diameter” per indicare il diamtro a petto d’uomo dell’albero monumentale. Se è incognito inserire un valore qualsiasi.
        • campo “name” per indicare il nome ed il cognome della persona che ha creato il dato (ovvero il nome dello studente)
        • campo “date” di tipo stringa, per indicare la data in formato anno/mese/giorno “YYYY/MM/DD” in cui è stata eseguita la misura del diametro (immaginando di aver eseguito il rilevamento in campo e non su google)
    2. Salvare in formato geoJSON il geodato creato al punto precedente:
      • path -> /home/Nome.Cognome/ (in questo path ciascuno ha i permessi per leggere e scrivere)
      • filename -> Nome_Cognome_alberoMonumentale
      • estensione del file -> quella del geoJSON (dovreste conoscerla…)
    3. Sincronizzatevi per una consegna interna vostra di tutti i file di cui al punto precedente nella cartella di interscambio indicata
    4. Ciascuno studente preleva i geodati di tutti gli altri + il proprio per creare un unico geodato vettoriale formando un catalogo di tutti gli alberi
    5. Rappresentare su mappa in R i punti (package tmap)
    6. Esportare da R il geodato relativo al catalogo di tutti gli alberi
    7. Scaricare da RStudio server
    8. Importare il geodato scaricato in QGIS e realizzare una mappa
    9. [OPZIONALE] Creare da zero il geodato dei punti in QGIS
    10. [OPZIONALE] Confrontare le due procedure, in R e QGIS
    11. Consegnare in RStudio al path “didattica/interscambio/es_01_create_SF/” il geodato del catalogo completo degli alberi (quindi ogni studente consegna il geodato con le info di tutti gli alberi). Denominare il file con il proprio nome e cognome per distinguerli.

23.2 Raster Geodata

23.2.1 Extract

Objective: use the geographical coordinates (got from Google maps) and extract the value of elevation from the raster having a different CRS.
Folder: ‘didattica/assignments/raster_ex01/’

Premise: the DEM is the digital elevation model in Telese Valley called dem5m_vt.tif.

Procedure:

  1. Import the Telese Valley dem in R, print the CRS and annotate its EPS code.
  2. Go to Google Maps.
  3. Get the geographical coordinates of a point within the Telese municipality.
  4. Write the Lat,Lon coordinates with at least 4 decimal numbers (e.g. 12.1234) in R.
  5. Create a vector data of class simple feature column (keep in mind the CRS definition), disregarding the definition of attributes.
  6. The point created above has a CRS: is it a GCS or PCS?
  7. Project the point according to the raster CRS.
  8. Extract from the raster the value of elevation at the geographical location given by the simple feature column created before.
  9. Save the R script with the procedure as name_surname_extract.R (e.g. giuliano_langella_extract.R) in the folder raster_ex01.

23.3 Create R functions

23.3.1 Let’s play dice!

Objective: learn how the sample() and replicate() functions work.
Folder: ‘didattica/assignments/function_ex01/’

Read section Writing Your Own Functions in the book Hands-On Programming with R.

23.3.1.1 The functions sample() and replicate()

  • sample( x, size, replace = FALSE, prob = NULL )
  • replicate( n, expr ) → see the examples provided in the book Hands-On Programming with R Chapter 3

23.3.1.2 Create a die with 6 faces: 

# create a die:
die = c(1,2,3,4,5,6)
# or, it's the same:
die = 1:6
die
#> [1] 1 2 3 4 5 6

23.3.1.3 let’s roll the die, once 

sample( die, 1 )
#> [1] 1
23.3.1.3.1 ONE die: 
# let's roll the die, 2 times
replicate( 2, sample( die, 1 ) )
#> [1] 2 3
# ...
# let's roll the die, 10 times
replicate( 10, sample( die, 1 ) )
#>  [1] 6 3 2 5 3 3 1 5 3 2
# you can get identical values, of course!
23.3.1.3.2 TWO dice (the argument replace is mandatory): 
# Deafault is for replace=FALSE, which means that the two
# random values will never be equal! 
sample( die, 2, replace=TRUE )
#> [1] 2 1
# Using replace=TRUE means that the extracted value is replaced again
# in the list, and we can choose the same value twice !
23.3.1.3.3 Roll the 2 dice as many times as the number of people in the room: who wins? 
N = 10
replicate( N, sample(die,2,replace=TRUE) )
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,]    2    4    5    2    3    4    5    1    4     4
#> [2,]    6    2    4    3    5    5    2    1    6     1

23.3.1.4 Create your own function: roll 2 dice

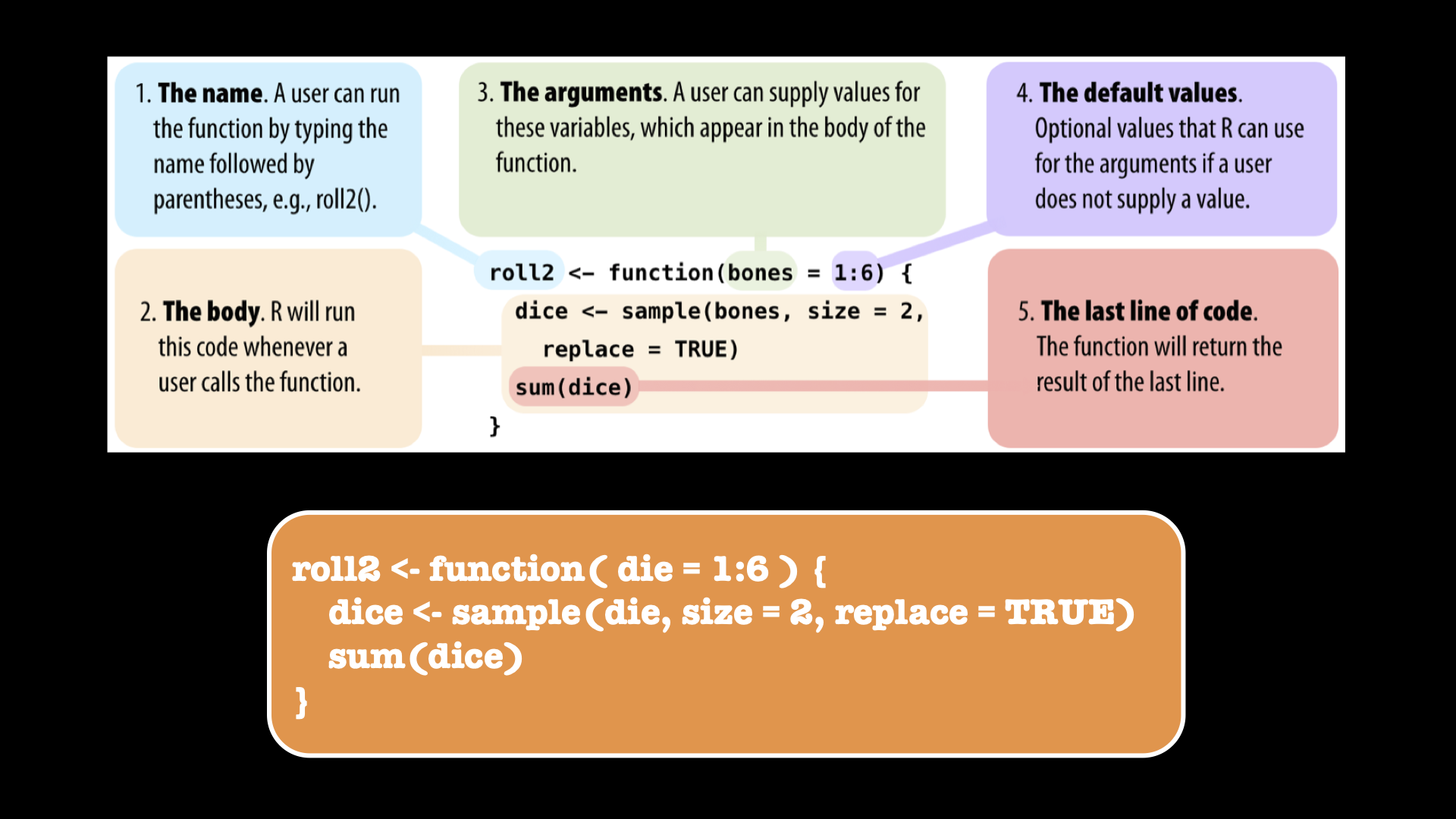
Create your own function.

Figure 23.1: Create your own function. 

roll2 <- function( die = 1:6 ) {
  dice <- sample(die, size = 2, replace = TRUE)
  sum(dice)
}

Let’s play:

roll2()
#> [1] 4

Roll the 2 dice as many times as the number of people in the room: who wins?

N = 12
replicate( N, roll2() )
#>  [1]  6  9  8  2  4  2 10  7  6  8  4  7

Roll the 2 dice to investigate the probability of each overall outcome:

library(ggplot2) # qplot function
rolls = replicate(1000, roll2())
ggplot2::qplot(rolls, binwidth = 1)
#> Warning: `qplot()` was deprecated in ggplot2 3.4.0.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where
#> this warning was generated.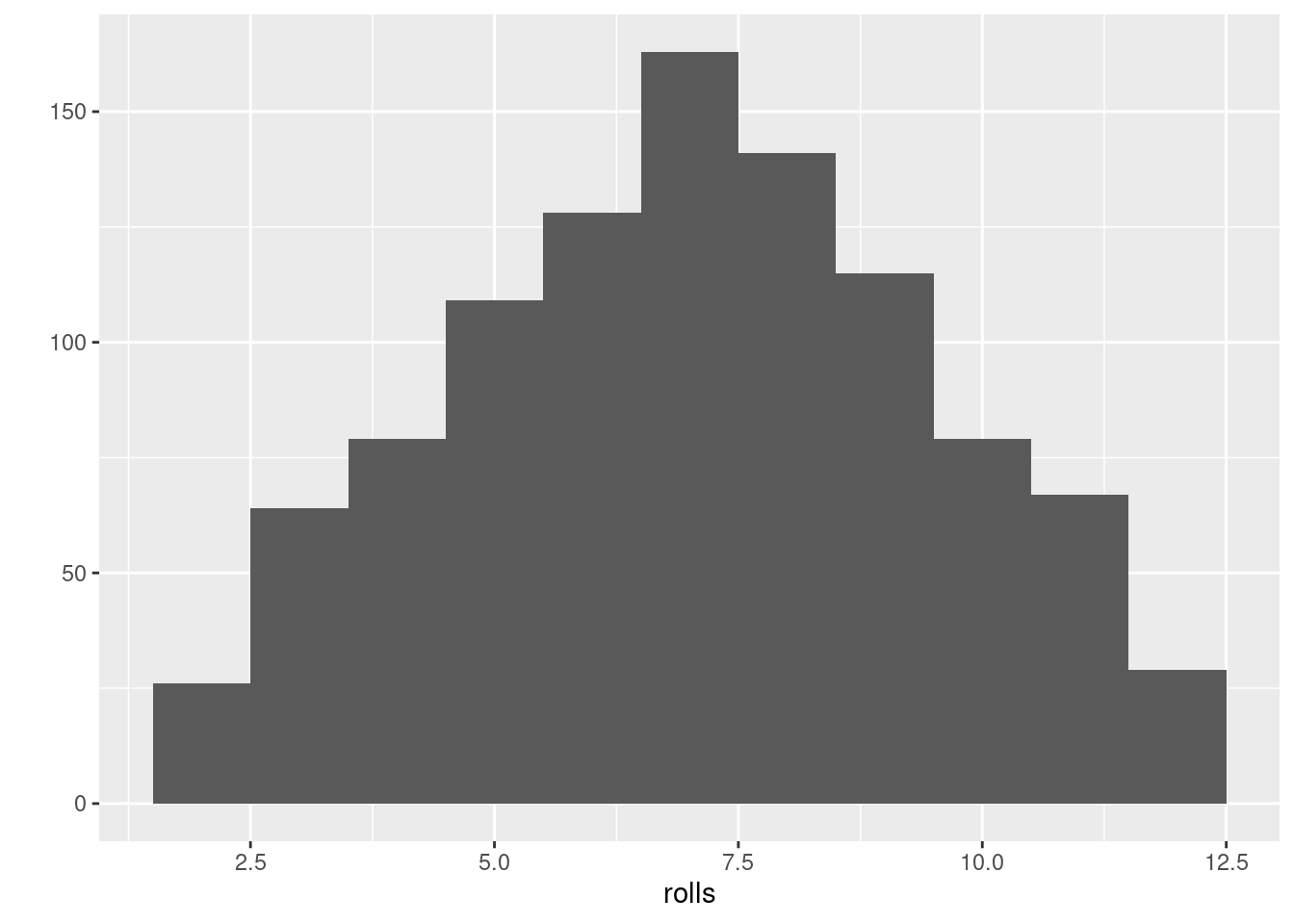

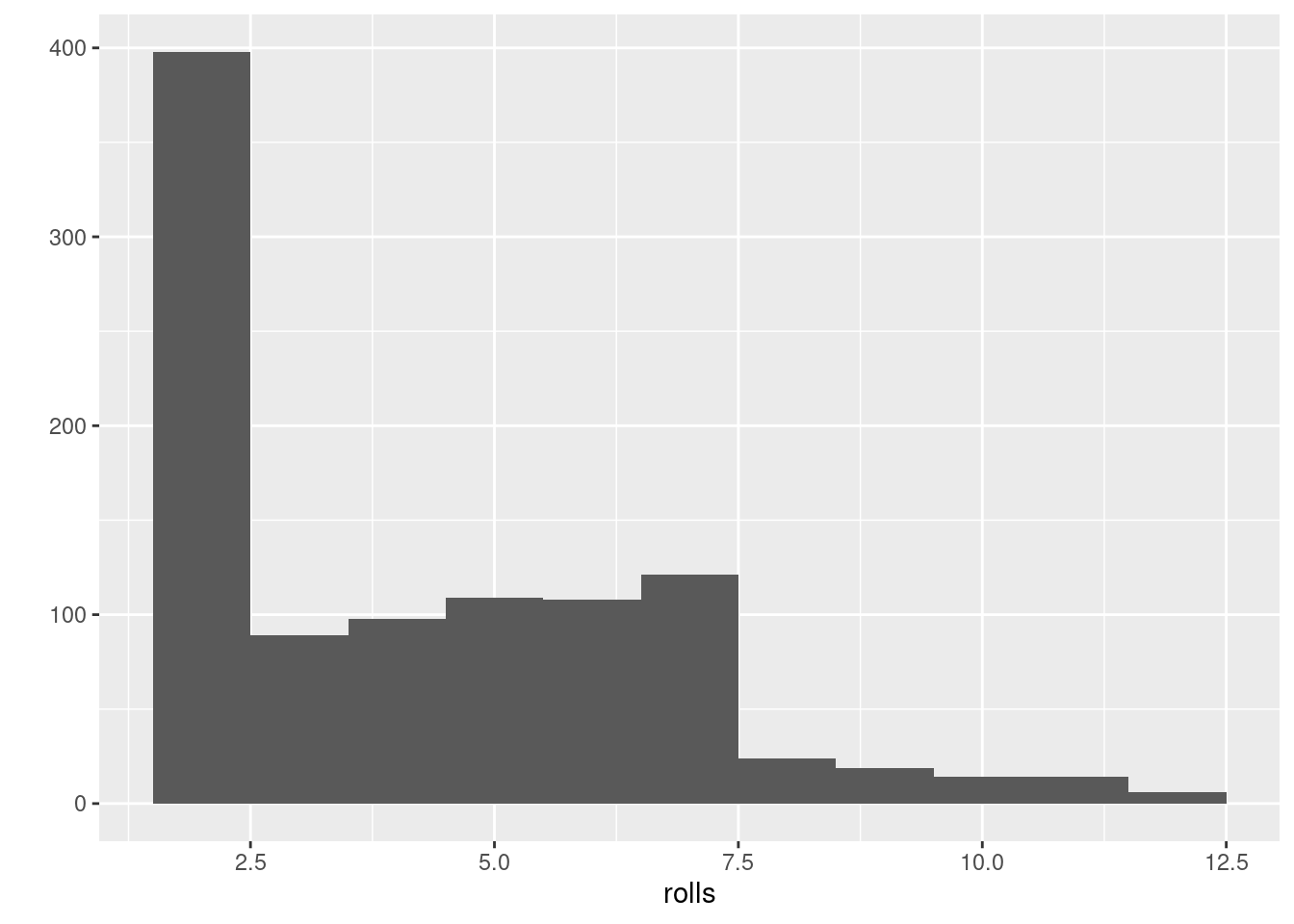
23.3.1.5 Let’s play using loaded dices

(Loaded dice = dado truccato)

roll2_loaded <- function( die = 1:6 ) {
  dice <- sample( die, size = 2, replace = TRUE, 
                  prob=c(9/14,1/14,1/14,1/14,1/14,1/14) )
  sum(dice)
}

Roll the 2 dice to investigate the probabilities for loaded dice: Who wins?

rolls = replicate(1000, roll2_loaded())
qplot(rolls, binwidth = 1)

23.3.1.6 Assignment

Create a script and save it in the folder function_ex01 defined above including the following elaboration:

  • Create a new script
  • Save the script as name_surname_dice.R in the assigned folder
  • Write the following commands in the script:
    • create a function to play with a die (un solo dado)
    • roll the die 20 times
    • store the results in a dedicated R object
    • report the number of times the die returned each number from one to six.
    • comment about the result
    • is there at least one number which was more frequent?
    • how many numbers and which were more frequent?

23.3.2 Create RMSE Error function

Objective: measure the goodness of a model.
Folder: ‘didattica/assignments/function_ex02/’

Create the following error function:

rmse <- function(M,P){
    # INPUTS
    #  M    : measurements
    #  P    : predictions
    
    # Checek that M & P have the same size:
    n1 <- length(M)
    n2 <- length(P)
    if(n1>n2 | n1<n2){
        print("Input vectors have different size!")
        return(NA)
    }
    
    n <- length(M)
    
    E = (M - P)
    S = E^2
    M = sum(S) / n
    R = sqrt(M)
    
    R # ---> return root mean square error
}

23.3.2.1 Assignment

Perform the following elaboration:

  • Create a new script and save it as name_surname_rmse.R in the folder function_ex02 defined above
  • Use the data provided in section height (H) and foot size (F) of students
  • Build a linear model between H (dep. var.) and F (indep. var.)
  • Interpolate the values of H given the F values provided
  • Measure the error of the model using the RMSE function created above

23.3.3 Create Pearson correlation function

Objective: measure the the level of linear dependence between two variables.
Folder: ‘didattica/assignments/function_ex03/’

Create the following error function:

myCorr = function(X,Y){
    nx = length(X)
    ny = length(Y)
    if (nx!=ny){
        stop('The length of inputs is different!')
    }else{
        n = nx
    }
    mu_x   = mean(X)
    mu_y   = mean(Y)
    COV_XY = sum( (X-mu_x)*(Y-mu_y) ) / n
    VAR_X  = sum( (X-mu_x)^2 ) / n
    VAR_Y  = sum( (Y-mu_y)^2 ) / n
    COV_XY / sqrt(VAR_X*VAR_Y) # --> return the correlation value
}

23.3.3.1 Assignment

Perform the following elaboration:

  • Create a new script
  • Import the soil temperature measurements provided in the file XY_Tmean.csv
  • Import the raster dem20m_campania.tif with elevation values for the whole Campania Region
  • Extract the elevation values from the raster at locations where the soil temperature values are available
  • Measure the level of linear dependence between the two variables soil temperature and elevation using the correlation function created above
  • save the script as name_surname_corr.R in the folder function_ex03 defined above

23.4 Raccolta ed analisi dei dati climatici

Objective: Manipolazione statistica dei dati agrometeorologici.
Folder: ‘didattica/assignments/agrimeteo_ex01/’
Source: ISPRA > SCIA > Serie Temporali Giornaliere

23.4.1 Raccolta

È possibile scaricare in formato CSV nuovi dati (temperatura e precipitazione) dal link fornito sopra.
I alternativa, utilizzare i dati di temperatura e precipitazione disponibili nei due file:

  • Tmax.xlsx
  • Rainfall.xlsx

23.4.2 Calcolare le seguenti statistiche

Dopo aver importato i dati (scaricati dal portale o presi dai file excel forniti) in Rstudio, eseguire le seguenti elaborazioni:

  • ricostruire eventuali dati mancanti calcolando la media nell’intorno,

  • per la serie giornaliera di un anno, calcolare le seguenti statistiche (per le statistiche mensili scegliere un mese a piacere diverso da gennaio):

    • Temperatura massima dell’aria
      • Valore minimo annuale e mensile
      • Valore massimo annuale e mensile
      • Valore medio annuale e mensile
      • Calcolare i gradi-giorno di una coltura/insetto a scelta
    • Precipitazione cumulata
      • Totale pioggia annuale e mensile
      • Numero di eventi piovosi annuale e mensile
      • Perturbazione (2 o più giorni) più piovosa nel mese selezionato

23.4.3 Ricostruzione dei dati mancanti di temperatura in una stazione

Eseguire le seguenti elaborazioni:

  • selezionare a caso ( sample() ) 10 giorni dell’anno per una stazione
  • conservare in un oggetto R distinto (original <- ...) le misure di temperatura di questi 10 giorni
  • cancellare i 10 valori selezionati scrivendo NO DATA VALUE,
  • costruire un modello di regressione lineare ( lm() ) tra la stazione selezionata (variabile dipendente) ed un’altra (variabile indipendente) con serie temporale completa (o senza dati mancanti nei 10 giorni che mancano nella var. dip.)
  • interpolare i valori mancanti usando i parametri del modello lineare di regressione
  • confrontare i valori interpolati con quelli originali (oggetto original) calcolando l’errore
    • calcolare la differenza tra il valore misurato e quello predetto
    • calcolare l’errore (MSE o RMSE)

23.4.4 Assignment

Perform the following elaboration:

23.5 Spatial interpolation

23.5.1 Few observations & manual interpolation

Objective: Spatial interpolation using basic R code and reasoning.
Folder: ‘didattica/assignments/spat_interp_ex01/’
Data: ‘didattica/docente_Langella/Data/xyCdDist.csv’ ; ‘didattica/docente_Langella/Data/xyCdDist_unknown.csv’

Please refer to the two CSV files listed under Data.

Use the cadmium concentration data provided in ‘xyCdDist.csv’ to perform spatial interpolations at the unknown location specified in ‘xyCdDist_unknown.csv’.

Develop an R script that implements the following spatial interpolation methods to predict the cadmium value at the unknown point:

  • Null model
  • Proximity polygon (Thiessen/Voronoi-based approach)
  • Nearest neighbors, using a maximum of 4 observations
  • Inverse Distance Weighting (IDW), using a maximum of 4 observations
  • Linear regression, using the variable dist (distance from the pollution source) as a predictor

Save and submit your script to the directory indicated under Folder above.

Tip: No additional libraries are required beyond base R. A bit of logical thinking will be enough to complete this exercise.

23.5.2 Cross-validation in single geospatial location

Objective: Spatial interpolation at one measured location.
Folder: ‘didattica/assignments/spat_interp_ex02/’
Data: ‘didattica/docente_Langella/Data/xyCdDist.csv’

Use the cadmium concentration data provided in ‘xyCdDist.csv’ to perform spatial interpolations at the geospatial location with row number 7.

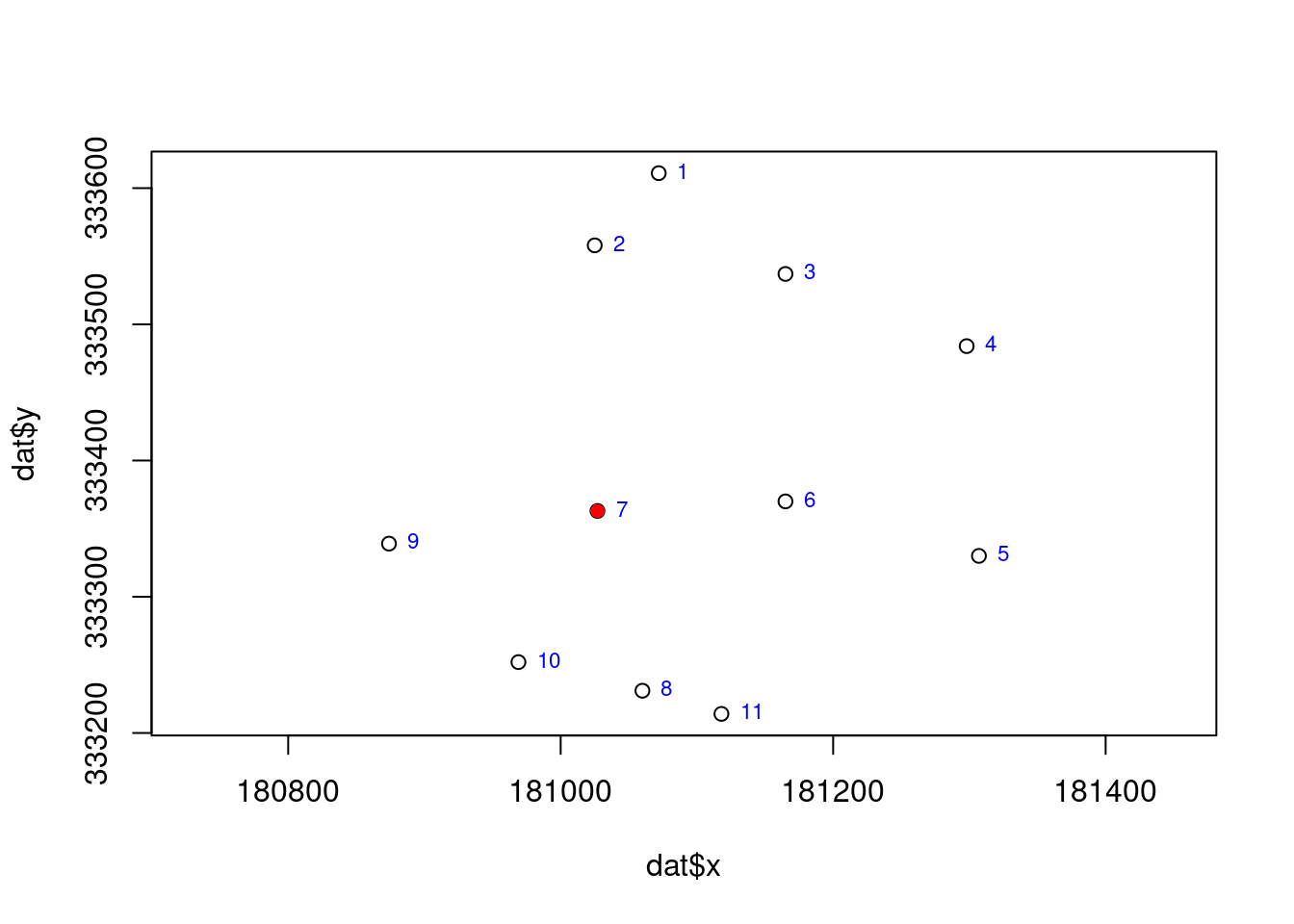
Develop an R script to implement the following spatial interpolation techniques for predicting cadmium concentration at the sampling point in row 7:

  • Null model
  • Proximity polygon (Thiessen/Voronoi-based approach)
  • Nearest neighbors, using a maximum of 4 observations
  • Inverse Distance Weighting (IDW), using a maximum of 4 observations
  • Linear regression, using the variable dist (distance from the pollution source) as a predictor

For each method, calculate the absolute error and decide about the most performing one.

Save and submit your script to the directory indicated under Folder above.

23.5.3 Cross-validation at all available geospatial locations

Objective: Spatial interpolation at all measured locations to enable cross validation.
Folder: ‘didattica/assignments/spat_interp_ex03/’
Data: ‘didattica/docente_Langella/Data/xyCdDist.csv’

Use the cadmium concentration data provided in ‘xyCdDist.csv’ to perform spatial interpolations at all geospatial locations. This exercise is identical to the previous one except that you have to extend what you did for measurement at row index 7 to all measurements.

Develop an R script to implement the following spatial interpolation techniques for predicting cadmium concentration at all sampling points:

  • Null model
  • Proximity polygon (Thiessen/Voronoi-based approach)
  • Nearest neighbors, using a maximum of 4 observations
  • Inverse Distance Weighting (IDW), using a maximum of 4 observations
  • Linear regression, using the variable dist (distance from the pollution source) as a predictor

For each method, calculate the RMSE and decide about the most performing one.

Save and submit your script to the directory indicated under Folder above.

23.6 Variography

23.6.1 Meuse assignment

Objective: Variography of meuse dataset and write commands and answers in a script.
Folder: ‘didattica/assignments/variography_ex01/’

Perform the following elaboration:

  • (load the required libraries)
  • Import the meuse built-in dataset
  • Analyse the content of object
    • Which class?
    • How many variables or attributes are available?
    • How many records are available?
    • Can you locate observations in spatial domain?
  • Transform into a simple feature
    • Check in the help for the CRS
    • Create a map using tmap to show the location of observations
    • Do you find a relationship of contamination with the Meuse River?
    • Describe this relationship…
  • Select a heavy metal different from Cadmium.
  • Create the cloud variogram and plot it
    • print in console the object containing the information about the cloud variogram
    • What does a single point in the chart represent? Explain in the script.
    • Which point in the chart has the highest distance value? Write in the script the distance value.
    • Which point in the chart has the highest variance value? Write the variance value in the script.
  • Create an experimental variogram and plot it
    • print in console the object containing the information about the experimental variogram
    • What does a single point in the chart represent? Explain in the script.
  • Perform a visual analysis of the experimental variogram in the chart and write the model variogram (using the vgm() function) which best fits the experimental one. This is a fitting made by eye.
    • print in console the object containing the information about the model variogram fitted by eye
  • Plot the experimental variogram and the one fitted by eye.
  • Perform the automatic fitting (using the fit.variogram() function) of the experimental variogram
    • print in console the object containing the information about the model variogram fitted automatically
  • Plot the experimental variogram and the one fitted automatically.
  • Compare the two model variograms fitted by eye and automatically: which one is working better and why?

Delivery

  • Create a new script
  • Fulfil the elaboration above
  • Save the script as name_surname_meuse.R (e.g. giuliano_langella_meuse.R) in the folder variography_ex01.

23.7 Regression tree

23.7.1 Assignment 1 — Introduction to Regression Trees

Objective:
Explore how to fit and interpret a regression tree using the BB.250 dataset.
The goal is to predict Soil Organic Carbon (SOC) based on available environmental covariates.

Folder: didattica/assignments/rtree_ex01/
Data: didattica/docente_Langella/Data/BB.250.csv


  1. Load the BB.250 dataset and inspect its structure (e.g., str(), summary(), head()).
  2. Build a regression tree model to predict SOC_target using the following predictors:
    x_25833, y_25833, Altitude, Slope, NDVI, GNDVI, ERa, G_Total_Counts, B08, B02.
  3. Plot the resulting tree and interpret its structure:
    • Which variable is used at the root split?
    • How many terminal nodes (leaves) are present?
    • What is the predicted SOC value in each leaf?
  4. Extract and display the variable importance from the model.
  5. Visualize the predicted SOC values as a map using ggplot2, tmap, or another mapping package. Optionally, compare the predicted spatial pattern to the actual SOC values using a scatterplot or residual map.


Expected outcome:
A practical understanding of how regression trees partition space, how important covariates are selected, and how spatial predictions can be visualized and interpreted.

23.7.2 Assignment 2 — Model Evaluation and Comparison

Objective:
Evaluate the performance of a regression tree model by comparing it to simpler interpolation methods using a training/validation split and RMSE.

Folder: didattica/assignments/rtree_ex02/
Data: didattica/docente_Langella/Data/BB.250.csv


  1. Split the BB.250 dataset into a training (80%) and validation (20%) subset using a random sampling strategy. Set a seed value to ensure reproducibility.
  2. Fit a regression tree model on the training subset to predict SOC_target using the same predictors as in Assignment 1:
    x_25833, y_25833, Altitude, Slope, NDVI, GNDVI, ERa, G_Total_Counts, B08, B02.
  3. Predict SOC values at the validation locations using the fitted regression tree model, and compute the RMSE using a custom function (e.g., rmse_v3).
  4. Compare the RMSE of the regression tree with that obtained from the following benchmark models:
    • Global mean model: predict the mean SOC value from the training set for all validation points
    • Nearest neighbour interpolation
    • Inverse Distance Weighting (IDW)
  5. Optionally, create maps of the residuals for each method to explore spatial patterns of under- or overestimation.


Expected outcome:
Ability to evaluate model accuracy using a validation subset, understand the limitations of global/statistical interpolators, and justify the use of machine learning approaches for spatial prediction.

  1. [see AG Journel and ChJ Huijbregts, Mining Geostatistics, The Blackburn Press (1978)]
    ↩︎
  2. [see T. Malvic and D. Balic, Linearity and Lagrange Linear Multiplicator in the Equations of Ordinary Kriging, NAFTA 59 (1) 31-37 (2009)]
    ↩︎