10 Regression

10.1 Install Packages

install.packages("Metrics")

10.2 Load Packages

library(Metrics)  # RMSE
library(readxl)   # import excel files
library(ggplot2)  # advanced plots

10.3 LINKS

Nice tutorial in R —> Beginners Guide to Regression Analysis and Plot Interpretations

There’s an error in the above webpage according to the definition of \(R^2\), which is:

\[R^2 = 1 - \frac{RSS}{TSS} = \frac{ESS}{TSS}\]

10.4 Introduction

The aim of linear regression is to model a continuous variable Y as a mathematical function of one or more X variable(s), so that we can use this regression model to predict the Y when only the X is known. This mathematical equation can be generalized as follows:

\[Y = \beta_{1} + \beta_{2}X + \epsilon\]

where, \(\beta_{1}\) is the intercept and \(\beta_{2}\) is the slope.
Collectively, they are called regression coefficients. \(\epsilon\) is the error term, the part of Y the regression model is unable to explain.

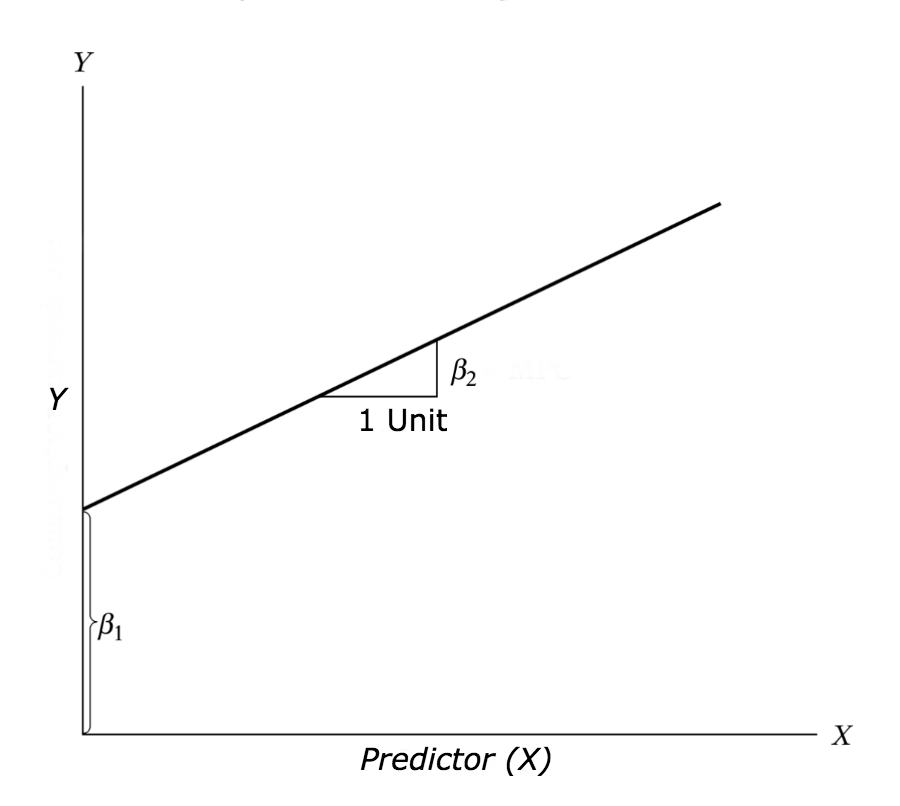
Figure 10.1: Linear regression explained.

10.5 Import Climatic Data [ \(T_{max}\), Rain ]

Tmax <- read_excel("../datasets/interchange/Tmax.xlsx", sheet = "measurements", na = "NA")
Rain <- read_excel("../datasets/interchange/Rainfall.xlsx", sheet = "measurements", na = "NA")

10.6 Scatter Plot

scatter.smooth( x=Tmax$MODENAURB, y=Tmax$SAGATABOAGRO, 
                main="SAGATABOAGRO ~ MODENAURB")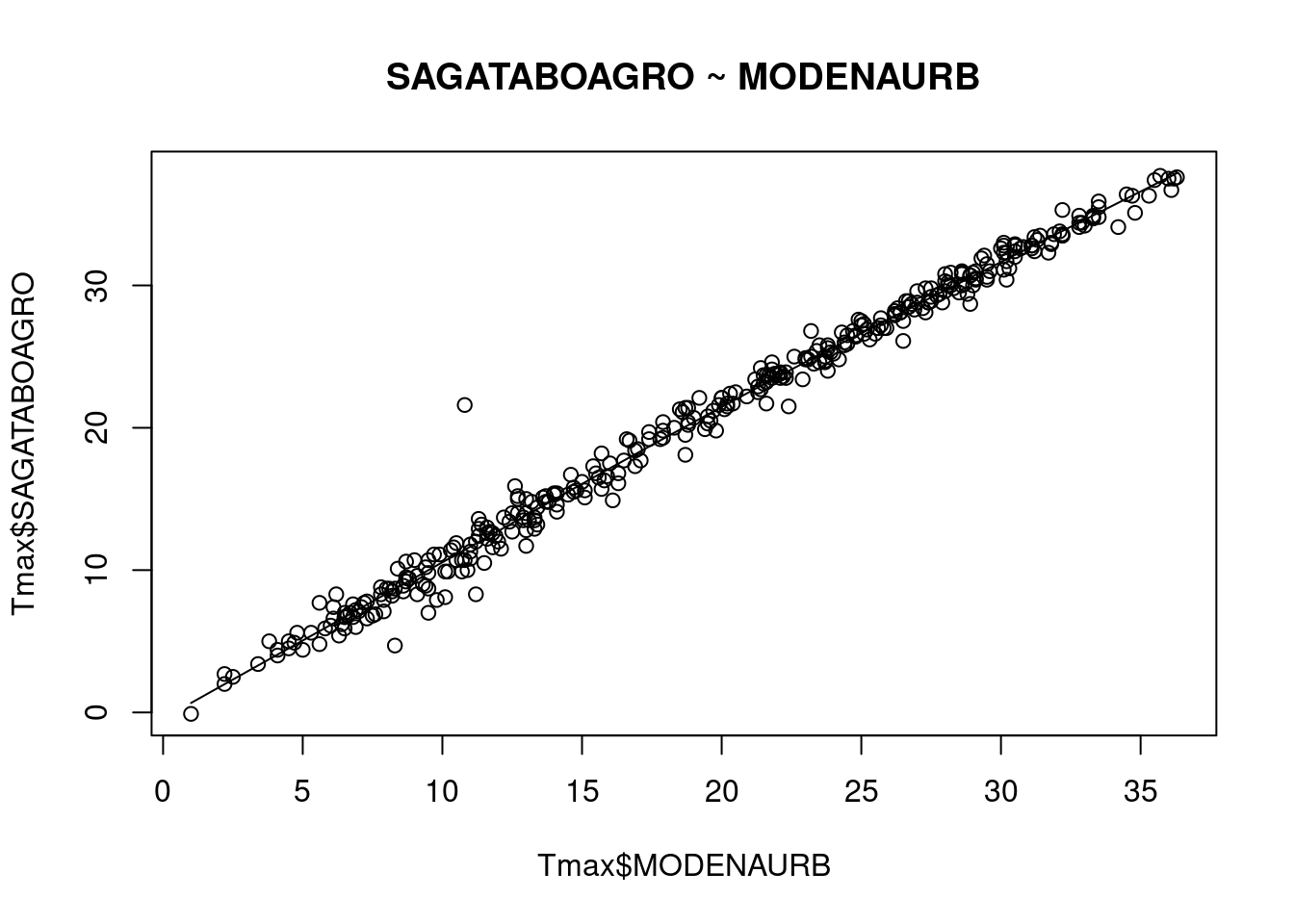

10.7 BoxPlot – Check for outliers

Generally, any datapoint that lies outside the 1.5 * interquartile-range (1.5 * IQR) is considered an outlier, where, IQR is calculated as the distance between the 25th percentile and 75th percentile values for that variable.

par(mfrow=c(1, 2))  # divide graph area in 2 columns
boxplot(Tmax$MODENAURB, main="MODENAURB", 
        sub=paste("Outlier rows: ", boxplot.stats(Tmax$MODENAURB)$out))
boxplot(Tmax$SAGATABOAGRO, main="SAGATABOAGRO", 
        sub=paste("Outlier rows: ", boxplot.stats(Tmax$SAGATABOAGRO)$out))

10.8 Density plot – Check if the response variable is close to normality

library(e1071)
par(mfrow=c(1, 2))  # divide graph area in 2 columns
plot(density(Tmax$MODENAURB), 
     main="Density Plot: MODENAURB", ylab="Frequency", 
     sub=paste("Skewness:", round(e1071::skewness(Tmax$MODENAURB), 2)))  
polygon(density(Tmax$MODENAURB), col="red")
plot(density(Tmax$SAGATABOAGRO), 
     main="Density Plot: SAGATABOAGRO", ylab="Frequency", 
     sub=paste("Skewness:", round(e1071::skewness(Tmax$SAGATABOAGRO), 2)))
polygon(density(Tmax$SAGATABOAGRO), col="red")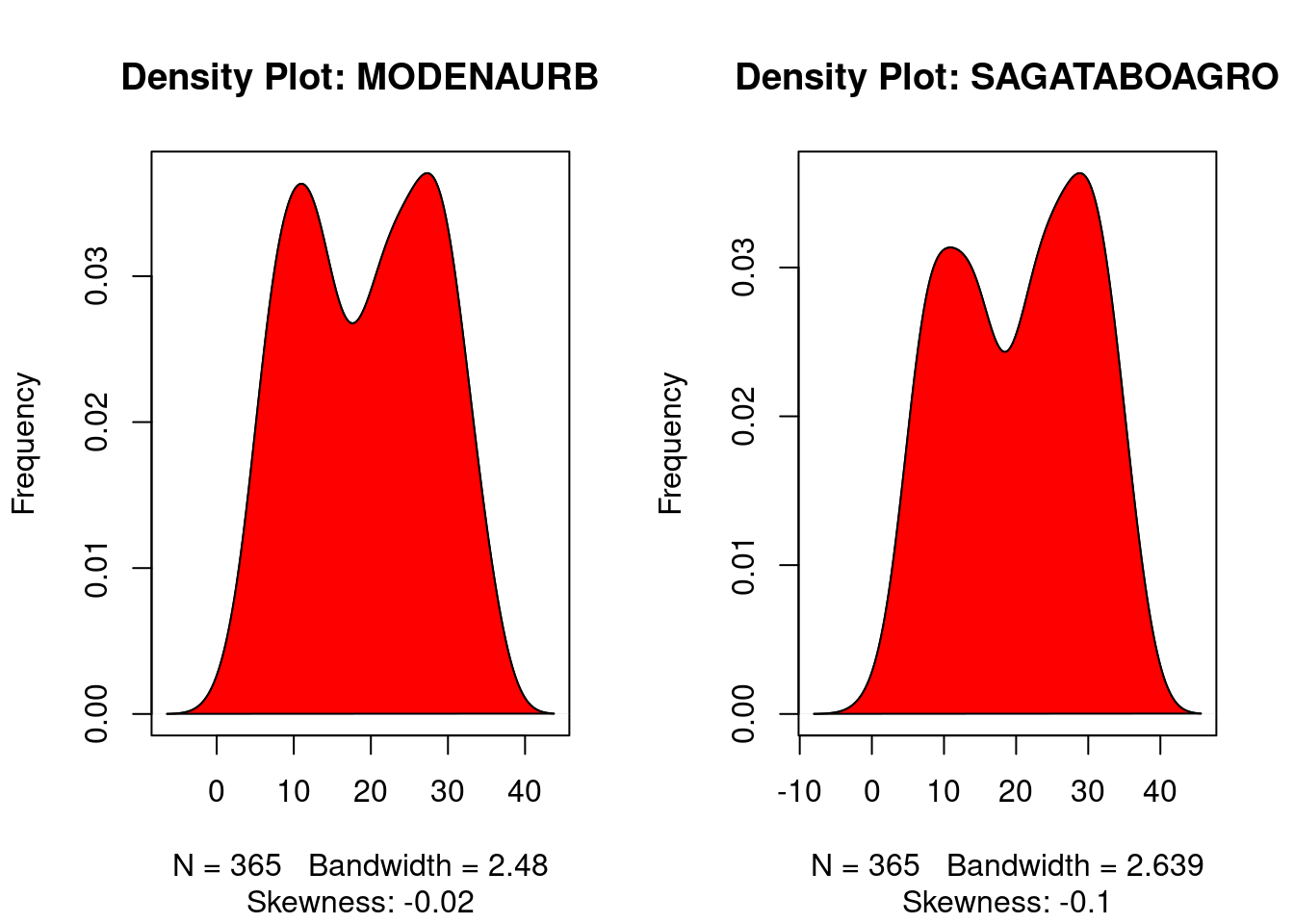

10.9 Build linear regression model on full data

linearMod <- lm(SAGATABOAGRO ~ MODENAURB, data=Tmax)
print(linearMod)
#> 
#> Call:
#> lm(formula = SAGATABOAGRO ~ MODENAURB, data = Tmax)
#> 
#> Coefficients:
#> (Intercept)    MODENAURB  
#>     0.03945      1.05787

summary(linearMod)
#> 
#> Call:
#> lm(formula = SAGATABOAGRO ~ MODENAURB, data = Tmax)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -4.1198 -0.4477  0.0439  0.4954 10.1355 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 0.039447   0.126553   0.312    0.755    
#> MODENAURB   1.057875   0.005932 178.326   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.015 on 363 degrees of freedom
#> Multiple R-squared:  0.9887, Adjusted R-squared:  0.9887 
#> F-statistic: 3.18e+04 on 1 and 363 DF,  p-value: < 2.2e-16

linearMod$coefficients
#> (Intercept)   MODENAURB 
#>  0.03944719  1.05787488

That is: \(Y = \beta_{1} + \beta_{2}X + \epsilon\)
\(SAGATABOAGRO = Intercept + (\beta ∗ MODENAURB)\)
\(SAGATABOAGRO = +0.03945 + 1.05787* MODENAURB\)

We have

• \(y_{i}\) observations;


• \(\overline{y}\) the average value;


• \(\hat{y_{i}}\) estimation from linear regression.

yi    = Tmax$SAGATABOAGRO
y_    = mean(yi)
y_hat = +0.03945 + 1.05787*Tmax$MODENAURB

10.9.1 Graphical visualization:

ggplot(Tmax, aes(x=MODENAURB, y=SAGATABOAGRO)) +
  geom_point(shape=18) +
  geom_smooth(method = "lm", se = FALSE, color="red") + 
  annotate("segment", x = 0, xend = max(Tmax$MODENAURB), 
           y = mean(Tmax$SAGATABOAGRO),
           yend = mean(Tmax$SAGATABOAGRO),  colour = "blue") +
  annotate("text", x = 0, y = 30, label = "yi : dati osservati",
           colour="black", hjust=0, vjust=0) +
  annotate("text", x = 0, y = 28, label = "y_hat : dati stimati dal modello",
           colour="red", hjust=0, vjust=0) +
  annotate("text", x = 0, y = 26, label = "y_ : valore medio",
           colour="blue", hjust=0, vjust=0)
#> `geom_smooth()` using formula = 'y ~ x'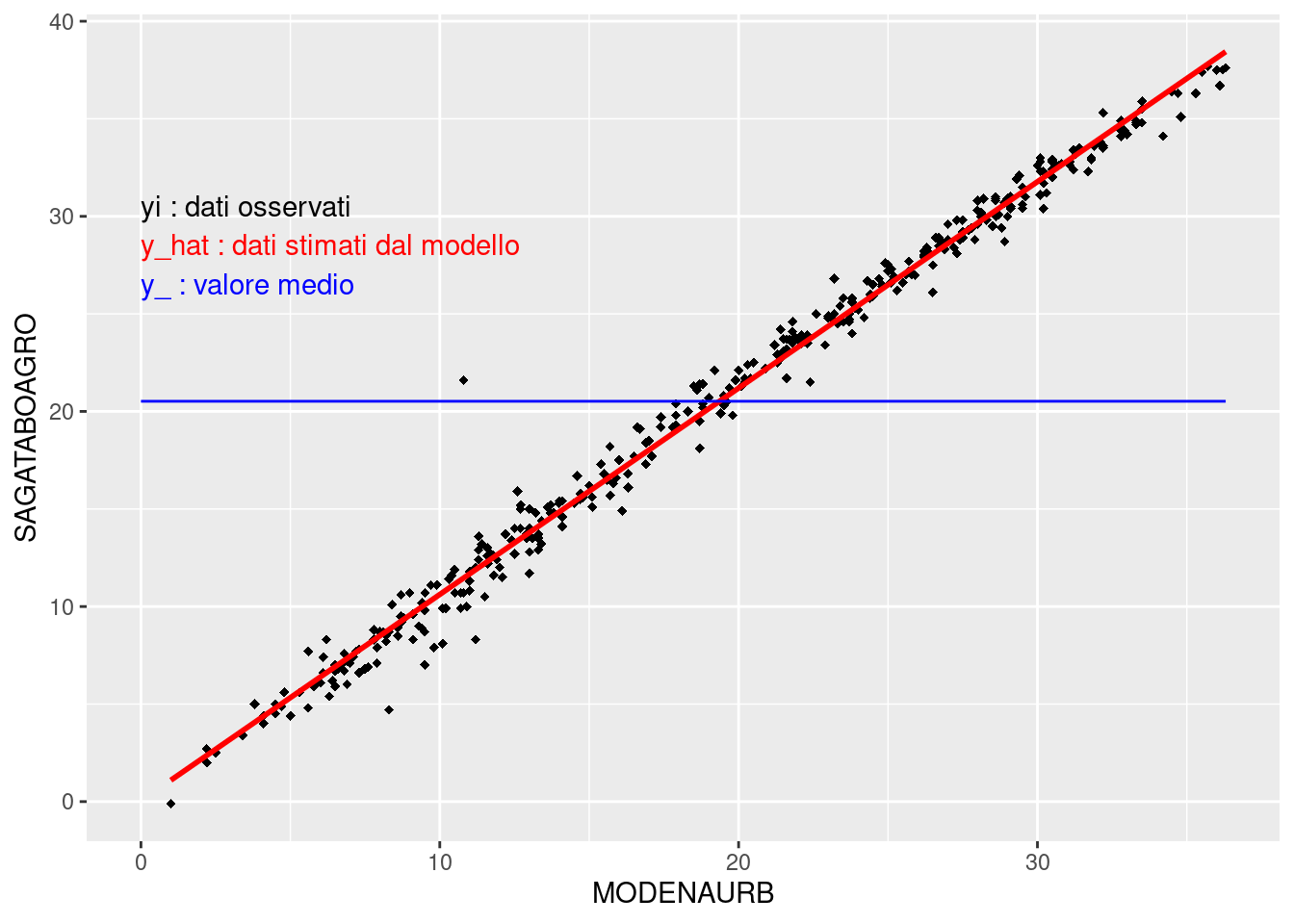

10.9.2 Deviance explained by the regression model (Explained Sum of Squares):

\[ESS = \sum_{i=1}^{n}\left( \hat{y_{i}}-\bar{y}\right)^{2}\]

ESS = sum( (y_hat-y_)^2 )
print(ESS)
#> [1] 32768.54

10.9.3 Total Deviance (Total Sum of Squares)

\[TSS = \sum_{i=1}^{n}\left( y_{i}-\bar{y}\right)^{2}\]

TSS = sum( (yi-y_)^2 )
print(TSS)
#> [1] 33142.9

10.9.4 Coefficient of determination

\[R^{2}=\frac{ESS}{TSS}\]

R2 = ESS / TSS
print(R2)
#> [1] 0.9887047

10.10 Linear regression model to infill missing data

10.10.1 Selezione della variabile dipendente o target da ricostruire:

yi = Tmax$SAGATABOAGRO # copia di SAGATABOAGRO da manipolare!
mean(yi)
#> [1] 20.52164

10.10.2 Rimozione di alcuni dati misurati, per simulare la presenza di dati mancanti:

NA_POS  = c(4,7,22,35,48,56,78,89,94,102,134,157,187,232,259,299,305,360)
MEAS_DATA = yi[NA_POS]
print( paste("No. of removed measurements: ",length(NA_POS)) )
#> [1] "No. of removed measurements:  18"
MEAS_DATA
#>  [1]  7.0  9.9  7.8  8.8 12.7 11.1 16.3  9.0 14.8 23.4 31.1
#> [12] 20.7 32.8 26.1 30.0 12.4 14.8  5.9

10.10.2.1 NA_POS

sample(1:365,20,replace=FALSE)
#>  [1] 203 103 325 314 114 130 120 104 275 204  63 339 169  85
#> [15] 261 181 323  99  54 263

sample(1:length(yi),20,replace=FALSE)
#>  [1]  77 225  65  44 179 362 285 196 151  72 172 182 263 221
#> [15] 298  11 316 351 332  30

10.10.2.2 Rimozione dati e scrittura di NA

yi[NA_POS] = NA # scrittura degli NA
yi[NA_POS] # stampa del contenuto di yi nelle posizioni in cui abbiamo scritto NA
#>  [1] NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA

10.10.3 Calcolo del valore medio:

y_ = mean(yi,na.rm=TRUE) # calcolo della media dopo rimozione degli NA scritti prima
# stampa il valore medio dopo scrittura di NA in yi
y_
#> [1] 20.73718
# stampa del valore media di yi prima della scrittura di NA
mean(Tmax$SAGATABOAGRO)
#> [1] 20.52164

10.10.4 Ricostruzione dei dati mancati: calcolo della media mobile

y_mm = (yi[NA_POS-1] + yi[NA_POS+1] ) / 2
y_mm
#>  [1] 12.40  9.45 12.00 12.50 11.65 14.45 13.40 15.20 19.60
#> [10] 24.10 27.65 24.95 31.20 26.90 28.75 13.50 16.75  5.25

yi[NA_POS[1]]
#> [1] NA

for(i in 1:length(NA_POS)){
    y_mm_students = mean(yi[NA_POS[i]-2] : yi[NA_POS[i]+2] , na.rm=TRUE )
}

10.10.5 Valori misurati rimossi, negli stessi giorni:

MEAS_DATA
#>  [1]  7.0  9.9  7.8  8.8 12.7 11.1 16.3  9.0 14.8 23.4 31.1
#> [12] 20.7 32.8 26.1 30.0 12.4 14.8  5.9

10.10.6 Ricostruzione dei dati mancati: regression lineare

10.10.6.1 Matrice X delle variabili indipendenti o covariate usate per ricostruire i dati mancanti

# Selezione delle stazioni di MODENAURB (pos=2) e CORREGGIOAGRO (pos=6)
X = Tmax[,c(2,6)]
summary(X)
#>    MODENAURB     CORREGGIOAGRO  
#>  Min.   : 1.00   Min.   :-0.20  
#>  1st Qu.:11.40   1st Qu.:11.50  
#>  Median :19.90   Median :21.00  
#>  Mean   :19.36   Mean   :20.15  
#>  3rd Qu.:27.30   3rd Qu.:28.50  
#>  Max.   :36.30   Max.   :37.10

10.10.6.2 Costruzione del modello di regressione tra la stazione da ricostruire e le altre disponibili:

yi[NA_POS] # questi sono i valori mancanti da ricostruire!
#>  [1] NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA

# build linear regression model using 1 covariate
lm1 <- lm(yi ~ X$MODENAURB)
print(lm1)
#> 
#> Call:
#> lm(formula = yi ~ X$MODENAURB)
#> 
#> Coefficients:
#> (Intercept)  X$MODENAURB  
#>     0.08073      1.05715

# build linear regression model using 2 covariate
lm2 <- lm(yi ~ X$MODENAURB + X$CORREGGIOAGRO)
print(lm2)
#> 
#> Call:
#> lm(formula = yi ~ X$MODENAURB + X$CORREGGIOAGRO)
#> 
#> Coefficients:
#>     (Intercept)      X$MODENAURB  X$CORREGGIOAGRO  
#>          0.1140           0.3612           0.6662

y_hat_1 = 0.06158 + 1.05783*X$MODENAURB[NA_POS]
y_hat_2 = 0.07883 + 0.35696*X$MODENAURB[NA_POS] + 0.67155*X$CORREGGIOAGRO[NA_POS]
#y_hat_2_bis = beta(1) + beta(2)*X$MODENAURB[NA_POS] + beta(3)*X$CORREGGIOAGRO[NA_POS]

beta = coefficients(lm1)

beta
#> (Intercept) X$MODENAURB 
#>  0.08073207  1.05714879

y_hat_1 = beta[1] + beta[2]*X$MODENAURB[NA_POS]
y_hat_1
#>  [1] 10.123646 10.757935  7.797918  8.326493 13.295092
#>  [6] 10.546505 16.783683  9.912216 14.669385 24.289439
#> [11] 31.900911 20.166559 32.958060 28.095175 30.738047
#> [16] 12.660803 14.563671  6.952199

beta = coefficients(lm2)

beta
#>     (Intercept)     X$MODENAURB X$CORREGGIOAGRO 
#>       0.1139654       0.3611984       0.6662450

y_hat_2 = beta[1] + beta[2] * X$MODENAURB[NA_POS] + beta[3] * X$CORREGGIOAGRO[NA_POS]
y_hat_2
#>  [1]  8.209065 10.757641  7.880800  8.128024 12.957007
#>  [6]  9.819283 16.480819  9.269442 15.158802 24.308663
#> [11] 31.373133 20.168385 32.800323 27.807586 29.976447
#> [16] 12.007419 15.322556  7.125470

cbind(y_,y_mm,MEAS_DATA,y_hat_1,y_hat_2)
#>             y_  y_mm MEAS_DATA   y_hat_1   y_hat_2
#>  [1,] 20.73718 12.40       7.0 10.123646  8.209065
#>  [2,] 20.73718  9.45       9.9 10.757935 10.757641
#>  [3,] 20.73718 12.00       7.8  7.797918  7.880800
#>  [4,] 20.73718 12.50       8.8  8.326493  8.128024
#>  [5,] 20.73718 11.65      12.7 13.295092 12.957007
#>  [6,] 20.73718 14.45      11.1 10.546505  9.819283
#>  [7,] 20.73718 13.40      16.3 16.783683 16.480819
#>  [8,] 20.73718 15.20       9.0  9.912216  9.269442
#>  [9,] 20.73718 19.60      14.8 14.669385 15.158802
#> [10,] 20.73718 24.10      23.4 24.289439 24.308663
#> [11,] 20.73718 27.65      31.1 31.900911 31.373133
#> [12,] 20.73718 24.95      20.7 20.166559 20.168385
#> [13,] 20.73718 31.20      32.8 32.958060 32.800323
#> [14,] 20.73718 26.90      26.1 28.095175 27.807586
#> [15,] 20.73718 28.75      30.0 30.738047 29.976447
#> [16,] 20.73718 13.50      12.4 12.660803 12.007419
#> [17,] 20.73718 16.75      14.8 14.563671 15.322556
#> [18,] 20.73718  5.25       5.9  6.952199  7.125470

10.10.7 Create two functions for error measurement:

Examples about how to create functions tailored to our needs.

10.10.7.1 RMSE (Root Mean Square Error)

# Function that returns Root Mean Squared Error
rmse <- function(M,P)
{
    sqrt(mean((M-P)^2))
}

10.10.7.2 MAE (Mean Absolute Error)

# Function that returns Mean Absolute Error
mae <- function(M,P)
{
    mean(abs(M-P))
}

10.10.8 Calculate RMSE

rmse(MEAS_DATA,y_)
#> [1] 9.619553
rmse(MEAS_DATA,y_mm)
#> [1] 3.193396
rmse(MEAS_DATA,y_hat_1)
#> [1] 1.053027
rmse(MEAS_DATA,y_hat_2)
#> [1] 0.7682606

10.10.9 Calculate MAE

mae(MEAS_DATA,y_)
#> [1] 8.783189
mae(MEAS_DATA,y_mm)
#> [1] 2.655556
mae(MEAS_DATA,y_hat_1)
#> [1] 0.7664819
mae(MEAS_DATA,y_hat_2)
#> [1] 0.5973194

Table 2.1: Compare measured values against interpolated ones.

y_	MEAS_DATA	y_mm		y_hat_1		y_hat_2
20.73718	7.0	12.40	5.40	10.123646	3.1236456	8.209065	1.2090649
20.73718	9.9	9.45	-0.45	10.757935	0.8579349	10.757641	0.8576413
20.73718	7.8	12.00	4.20	7.797918	-0.0020817	7.880800	0.0807999
20.73718	8.8	12.50	3.70	8.326493	-0.4735073	8.128024	-0.6719764
20.73718	12.7	11.65	-1.05	13.295092	0.5950920	12.957007	0.2570074
20.73718	11.1	14.45	3.35	10.546505	-0.5534949	9.819283	-1.2807169
20.73718	16.3	13.40	-2.90	16.783683	0.4836830	16.480819	0.1808194
20.73718	9.0	15.20	6.20	9.912216	0.9122159	9.269442	0.2694416
20.73718	14.8	19.60	4.80	14.669385	-0.1306146	15.158802	0.3588022
20.73718	23.4	24.10	0.70	24.289440	0.8894395	24.308663	0.9086632
20.73718	31.1	27.65	-3.45	31.900911	0.8009108	31.373133	0.2731329
20.73718	20.7	24.95	4.25	20.166559	-0.5334408	20.168385	-0.5316149
20.73718	32.8	31.20	-1.60	32.958060	0.1580596	32.800323	0.0003233
20.73718	26.1	26.90	0.80	28.095175	1.9951751	27.807586	1.7075858
20.73718	30.0	28.75	-1.25	30.738047	0.7380471	29.976447	-0.0235528
20.73718	12.4	13.50	1.10	12.660803	0.2608027	12.007419	-0.3925811
20.73718	14.8	16.75	1.95	14.563671	-0.2363294	15.322556	0.5225558
20.73718	5.9	5.25	-0.65	6.952199	1.0521992	7.125470	1.2254697

10.10.10 Use our function to measure the error

rmse(MEAS_DATA,y_)
#> [1] 9.619553

10.10.11 Use a dedicated package to measure the error

Metrics::rmse(MEAS_DATA,y_)
#> [1] 9.619553

10.10.12 Are there differences?

Answer…