20 Regression Tree

Understanding regression trees for environmental and spatial data modeling.

20.1 Introduction

In the context of spatial prediction and data modeling, regression trees represent a flexible, intuitive, and robust approach for dealing with non-linear relationships, missing values, and complex interactions between variables.

Unlike traditional regression models, which assume a specific mathematical form between predictors and the response, regression trees work by recursively splitting the data into increasingly homogeneous subsets based on the values of the predictor variables. These splits lead to a tree-like structure, where each terminal node (or “leaf”) corresponds to a predicted value.

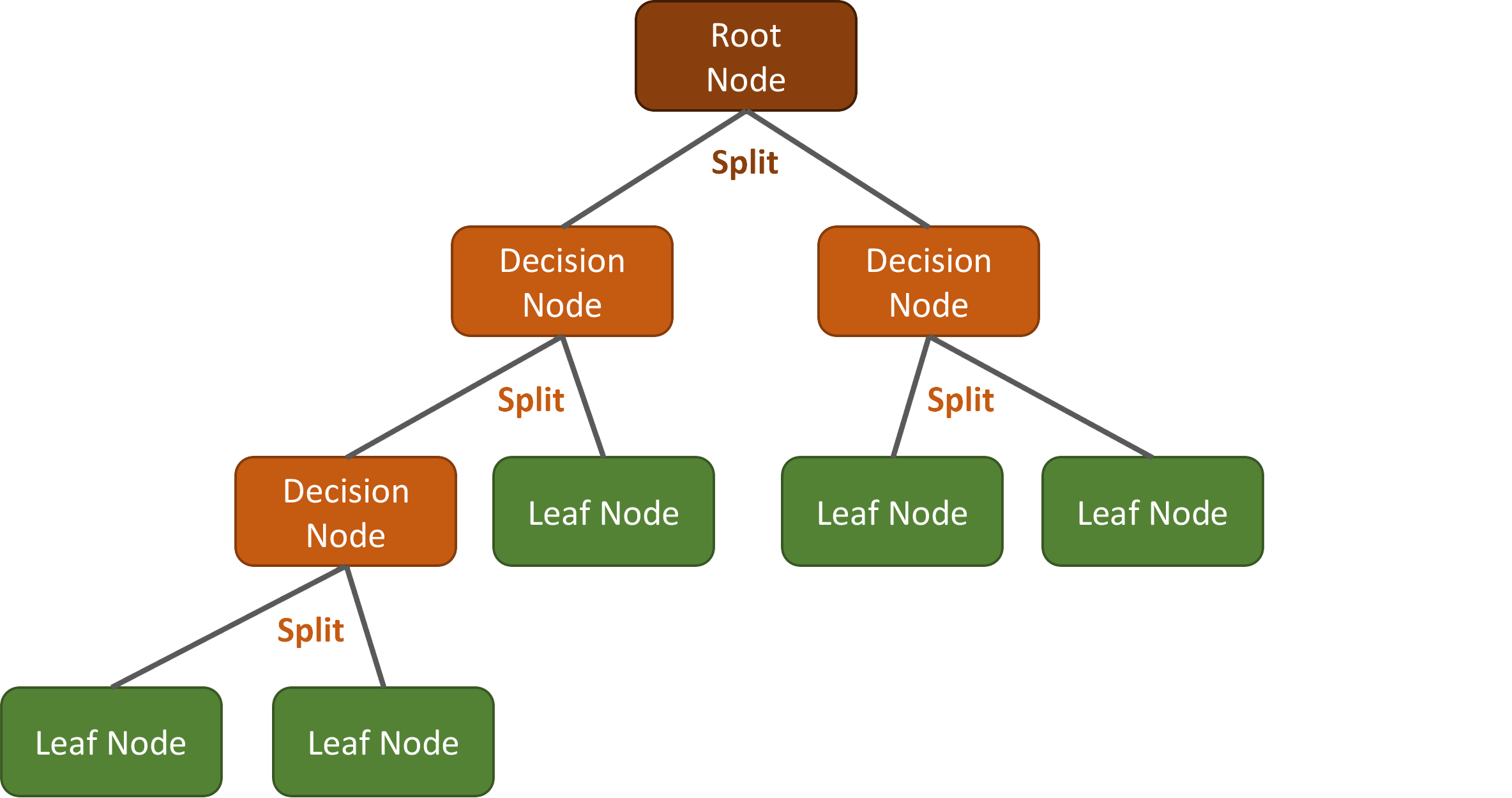
Figure 20.1: General structure of regression tree.

This method has gained popularity across ecological, agricultural, and environmental sciences due to its interpretability, minimal assumptions, and ability to model intricate patterns — including threshold effects and interactions — without requiring prior data transformation or feature engineering. Although not inherently spatial, regression trees can be adapted for spatial data modeling by including coordinate variables or combining with geostatistical techniques.

20.2 Why is it called a “regression tree”?

Let’s break down the term “regression tree” into its two parts.

First, it is called a tree because the model is structured like a decision tree: it starts from a single root and branches out recursively based on “yes/no” or “greater/less than” questions about the predictor variables. Each split leads to a new branch, and each end-point (leaf) of the tree contains a group of data points with similar characteristics. In practice, it feels like playing a decision game:

“Is the slope greater than 20%?”
“Is NDVI less than 0.4?”
and so on

Each question progressively refines the prediction.

Second, it is a regression tree because it is used to predict a continuous numeric outcome — such as soil organic carbon, mean temperature, or biomass — as opposed to a classification tree, which predicts categorical outcomes (e.g., species type, land cover class, see figure below).

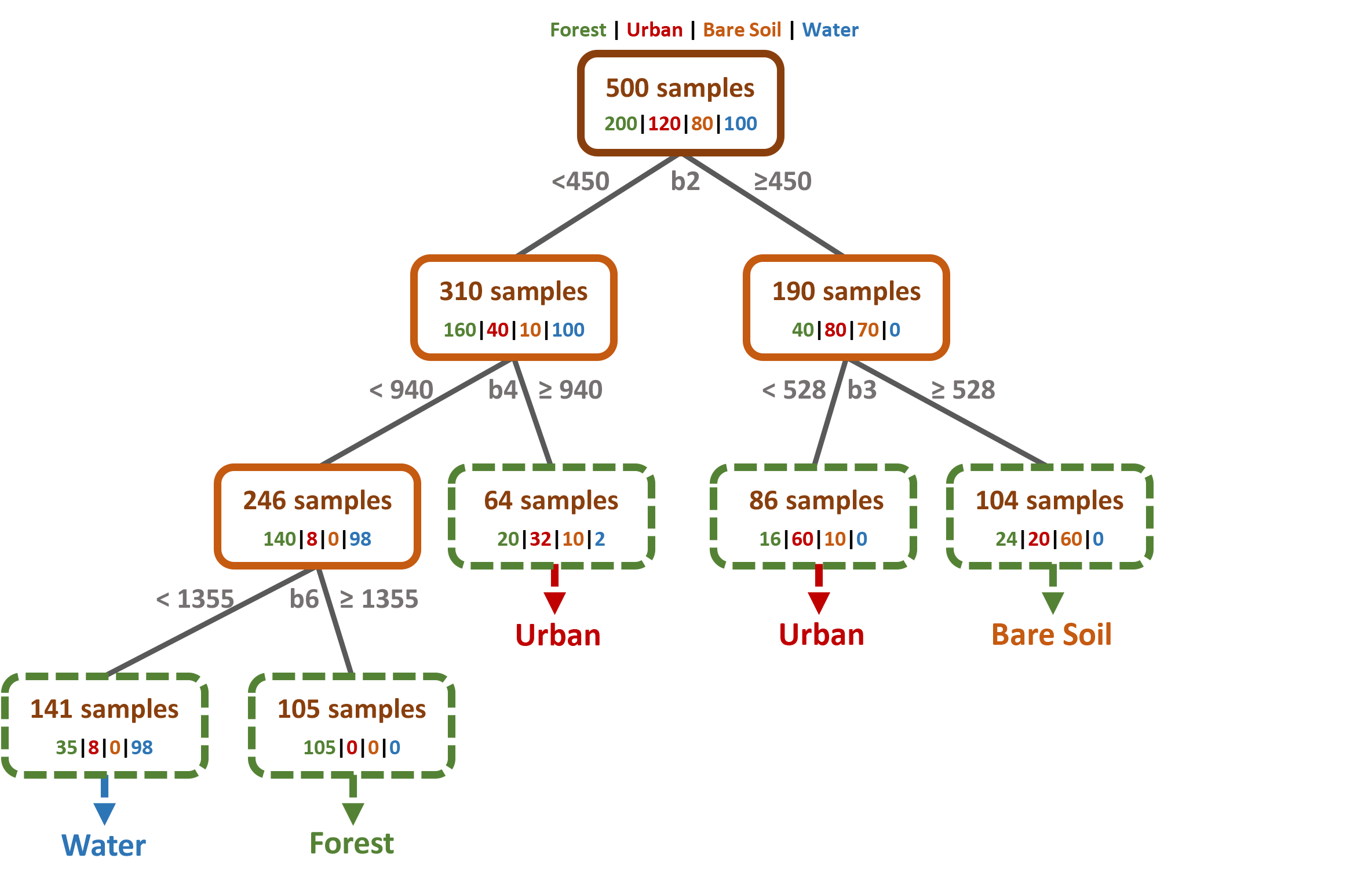
Figure 20.2: Classification tree to predict land cover.

Within each leaf, the output is typically the average of the target variable for the observations falling in that group. In this sense, a regression tree is a way to learn “piecewise constant” functions — it doesn’t output a smooth mathematical equation, but a series of rule-based decisions that result in constant predictions for each region of the predictor space.

20.3 How does a regression tree work?

The core principle of a regression tree is a recursive binary partitioning of the data based on predictor variables. The algorithm searches for the optimal threshold in one of the variables that best splits the dataset into two groups, such that the variability within each group is minimized. This split is chosen by evaluating all possible thresholds for each variable and selecting the one that results in the greatest reduction of prediction error.

The most common criterion used for this purpose is the minimization of intra-node variance, i.e., the average squared deviation of the response values from their node mean. In other words, at each step, the algorithm seeks the split that creates child nodes that are as homogeneous as possible in terms of the target variable.

This process continues recursively until a stopping condition is met: for instance, a minimum number of observations in each leaf, or a minimum improvement in error reduction. However, if the tree is allowed to grow too deep, it may start to overfit the training data — that is, it memorizes noise or very specific patterns that do not generalize to new data. To prevent this, the tree can be pruned, i.e., simplified by cutting back some of the branches, often based on cross-validation or a complexity parameter, in order to strike a better balance between bias and variance.

20.4 Implementation in R

Regression trees can be implemented in R using the well-established rpart package. Visualization can be handled with rpart.plot.

20.4.1 Required packages

library(rpart)        # for model fitting
library(rpart.plot)   # for tree visualization

20.4.2 Import a dataset

Assuming we have a spatial dataset with covariates and a target variable:

BB.250 <- read.csv('datasets/BB.250.csv')

20.4.2.1 Dataset Overview

This dataset contains a variety of variables derived from laboratory analysis, remote sensing, and spatial modeling. A concise description of the variable groups is provided below:

Target variables: SOC, pH, and Clay are laboratory-measured properties and serve as the prediction targets.
Digital Elevation Model (DEM): Derived from LiDAR and photogrammetric data with a spatial resolution of 5 meters.
Geophysical measurements: Apparent Electrical Resistivity (ERa) and Gamma Radiation (Total Counts) were collected in the field and interpolated using ordinary kriging.
Reflectance Spectral Signals (RSS): Sentinel-2 spectral bands acquired over bare soil conditions.
Vegetation Indices (VI): Indices such as NDVI and GNDVI derived from Sentinel-2 data during the vegetation season.

Table 20.1: BB.250 Dataset (Full Table)
X	x_25833	y_25833	SOC_target	pH_target	Clay_target	Altitude	Slope	ERa	G_Total_Counts	pH_ISE	B02	B03	B04	B05	B06	B07	B08	B8A	B11	B12	NDVI	GNDVI
1	463123.2	5804705	0.84	6.3	5.1	72.55	0.2612495	283.88306	1170.5445	6.732892	2019	2368	2852	3143	3560	3624	3714	3797	4524	4550	0.4741913	0.4661191
2	463169.1	5804694	0.61	6.0	3.4	72.34	0.2425003	304.21622	1185.2359	6.733316	2010	2310	2798	2972	3141	3265	3526	3524	4711	4822	0.4374892	0.4382333
3	463144.1	5804738	0.79	6.2	4.1	70.45	0.1812496	406.82909	1256.4166	6.778458	1988	2310	2810	3081	3203	3352	3634	3650	4873	4876	0.4824103	0.4680924
4	463169.1	5804781	0.77	6.7	4.8	68.03	0.2049990	341.54785	1232.3249	6.761032	1972	2306	2798	3006	3136	3432	3622	3648	4883	4945	0.4607366	0.4642982
5	463169.1	5804868	0.65	5.9	2.8	65.49	0.1837492	405.41499	1257.7680	6.551815	2038	2368	2862	3103	4306	4521	3728	4727	3696	3468	0.3994159	0.4273699
6	463198.2	5804662	0.58	5.9	3.5	74.23	0.1199999	533.85242	1132.7383	6.668399	1992	2368	2802	3042	3194	3314	3540	3533	4677	4790	0.3997243	0.4084605
7	463219.1	5804694	0.65	6.3	4.0	71.59	0.2487507	909.92277	1131.9628	6.725732	2042	2346	2826	3053	3197	3363	3598	3598	4868	5031	0.3683481	0.3853984
8	463194.1	5804738	0.58	6.4	3.2	70.00	0.1700010	366.57248	1080.6674	6.782501	2012	2332	2820	2986	3107	3275	3584	3504	4738	4884	0.4045643	0.4168120
9	463219.1	5804781	0.66	6.4	3.9	67.06	0.2250004	434.28382	1133.3119	6.741455	1977	2302	2748	2983	3137	3273	3500	3471	4789	4919	0.4356174	0.4422226
10	463194.1	5804824	0.64	6.4	4.3	65.94	0.1324997	475.84408	1208.5534	6.676767	1958	2230	2742	3054	3234	3440	3520	3647	4890	5036	0.4456290	0.4433209
11	463219.1	5804868	0.73	6.4	3.8	64.05	0.1224990	438.88875	1237.7501	6.590428	1910	2182	2650	2664	2770	2960	3392	3241	4670	4819	0.4405844	0.4375111
12	463194.1	5804911	0.95	6.1	5.5	63.06	0.1562495	331.31542	1294.4736	6.541923	1845	2070	2450	2830	3623	3857	3202	4182	3968	3721	0.4912594	0.4736471
13	463219.1	5804954	1.01	6.6	4.2	61.28	0.1224995	338.62425	1304.2030	6.652365	1868	2090	2448	2680	2852	2959	3222	3213	4576	4711	0.5242091	0.5034483
14	463148.8	5804816	0.8	6.4	4.4	67.52	0.0800009	540.47264	1263.1579	6.679825	1956	2464	2814	3139	3962	4067	4256	4307	4223	4139	0.3861518	0.3799503
15	463274.1	5804622	0.62	6.2	3.0	74.47	0.0937500	208.93547	1093.6202	6.619129	1982	2310	2758	3060	3142	3383	3524	3584	4761	4806	0.4495173	0.4478588
16	463244.1	5804651	0.54	6.3	2.1	74.33	0.3012514	354.53489	1091.6328	6.641480	1966	2302	2752	3042	3129	3341	3492	3563	4741	4834	0.4039801	0.4110000
17	463269.1	5804694	0.52	6.5	2.6	70.56	0.2824993	502.64409	1064.3973	6.718485	1963	2252	2716	3000	3107	3257	3444	3512	4773	4944	0.4022263	0.4052614
18	463244.1	5804738	0.58	6.3	4.7	69.00	0.2587500	485.50856	1161.6833	6.761165	1975	2308	2770	3019	3156	3279	3530	3530	4859	5008	0.3899130	0.4115154
19	463269.1	5804781	0.67	6.0	2.9	66.04	0.1875000	444.01528	1083.5679	6.676435	1974	2280	2736	2995	3128	3300	3512	3513	4896	5032	0.4647090	0.4644499
20	463244.1	5804824	0.71	5.9	1.8	64.94	0.1937513	675.96647	1154.2355	6.613087	1943	2222	2692	2942	3075	3259	3460	3488	4849	5001	0.4637707	0.4588361
21	463269.1	5804868	0.78	5.5	3.7	63.23	0.1362500	561.34947	1225.7150	6.554564	1890	2148	2584	2660	2770	2977	3346	3216	4674	4836	0.4828080	0.4806867
22	463244.1	5804911	0.96	5.9	3.6	62.21	0.1562495	417.46456	1282.2523	6.647943	1784	2004	2354	2596	2738	2893	3042	3143	4562	4768	0.4909617	0.4694459
23	463269.1	5804954	0.93	6.8	4.6	60.41	0.1274996	261.55423	1227.9391	6.866014	1848	2046	2410	2545	2720	2852	3124	3073	4307	4483	0.5223775	0.4940972
24	463244.1	5804997	1.13	7.2	7.2	60.17	0.0924993	214.22471	1327.4956	6.861070	1788	2010	2360	2451	2605	2749	3002	2911	3926	4027	0.5403641	0.5184558
25	463262.6	5805028	1.36	6.8	6.9	59.14	0.1012497	136.53027	1350.7741	7.019144	1711	1866	2168	2361	2511	2725	2792	2953	3982	4011	0.5454386	0.5156008
26	463237.6	5805071	1.19	6.4	5.7	59.17	0.0549994	178.96968	1342.0250	6.878581	1667	1948	2152	2397	2910	3345	3336	3579	3737	3651	0.4664790	0.4473776
27	463262.6	5805115	1.75	7.2	9.3	58.68	0.1062498	87.62483	1406.8092	7.019442	1608	1800	2094	2185	2570	2655	2846	2896	3772	3686	0.6139351	0.5694487
28	463319.1	5804608	0.81	6.4	8.8	74.10	0.0962486	57.80892	1238.1165	6.670382	1892	2178	2636	2943	3051	3254	3254	3430	4598	4554	0.4856771	0.4765448
29	463294.1	5804651	0.66	5.8	2.4	72.18	0.3974991	514.80166	1056.4696	6.676565	2036	2364	2832	3014	3165	3306	3624	3529	4789	4838	0.4769028	0.4651011
30	463319.1	5804694	0.63	5.9	4.9	68.51	0.2425003	629.99310	1075.5188	6.777109	1980	2296	2764	2956	3079	3255	3544	3498	4800	4922	0.4438503	0.4424040
31	463294.1	5804738	0.61	6.5	3.8	67.23	0.2325001	589.01161	1109.2969	6.753284	1954	2224	2692	2986	3073	3259	3424	3494	4824	4959	0.4498991	0.4416583
32	463319.1	5804781	0.79	5.7	3.5	65.23	0.1312504	309.97155	1192.6653	6.650025	1968	2274	2720	2990	3099	3246	3478	3516	4844	4981	0.5283514	0.5068670
33	463294.1	5804824	0.81	5.4	3.2	64.16	0.1262498	655.00111	1205.6820	6.520656	1955	2248	2742	2980	3113	3273	3502	3513	4879	4999	0.5339806	0.5096356
34	463319.1	5804868	0.91	5.7	4.5	62.33	0.1725001	367.96985	1241.3692	6.517238	1890	2168	2608	2754	2883	3076	3404	3335	4763	4888	0.5224681	0.5008264
35	463294.1	5804911	0.96	5.7	4.7	60.95	0.2187505	350.15519	1292.8367	6.707912	1921	2130	2544	2674	2786	2939	3276	3203	4580	4766	0.5276663	0.5181266
36	463319.1	5804954	1.43	7.1	7.2	59.44	0.0587506	136.67012	1408.1845	7.004392	1827	1984	2306	2432	2542	2698	2970	2868	3903	3992	0.6195200	0.5852780
37	463294.1	5804997	1.48	7.1	6.7	59.03	0.1737499	115.22693	1326.0413	7.119768	1674	1820	2088	2385	2510	2668	2696	2827	3804	3902	0.6429232	0.6091815
38	463312.6	5805028	1.64	7.2	7.6	58.43	0.1037502	55.81483	1363.2977	7.286209	1634	1776	2042	2223	2345	2524	2632	2738	3950	3945	0.6517205	0.6151493
39	463287.6	5805071	1.85	7.3	10.8	58.36	0.0450001	77.63236	1339.8493	7.190218	1697	1869	2182	2324	2509	2707	2882	2919	4006	3956	0.6596882	0.6237653
40	463312.6	5805115	1.69	7.2	11.7	58.26	0.0525012	65.78011	1292.3300	7.213527	1610	1776	2046	2196	2375	2506	2692	2767	3922	3905	0.6601539	0.6215122
41	463287.6	5805158	1.39	7.1	9.4	58.87	0.1137505	83.23549	1320.5339	7.016883	1634	1842	2080	2224	2344	2485	2852	2756	4034	3892	0.5890183	0.5510801
42	463312.6	5805201	1.17	6.6	8.1	59.56	0.0787506	120.49092	1324.9824	6.910338	1704	1870	2182	2457	2512	2750	2974	3003	4304	4214	0.5649516	0.5329341
43	463312.6	5805288	0.89	6.9	6.0	59.87	0.0274997	320.48392	1338.5972	6.854764	1944	2238	2676	2721	4372	4869	3530	5017	3115	2854	0.4953011	0.4981691
44	463369.1	5804608	0.89	6.1	10.4	72.79	0.2174997	225.09859	1089.7800	6.762279	1872	2152	2584	2885	3018	3151	3262	3348	4459	4423	0.5095323	0.4862827
45	463344.1	5804651	0.71	6.4	7.9	70.04	0.3349991	531.28283	1068.2773	6.766811	2011	2310	2802	2963	3055	3287	3510	3460	4599	4714	0.4265641	0.4327957
46	463369.1	5804694	0.79	6.5	3.8	67.14	0.1900005	547.76121	1049.8085	6.793718	1908	2210	2640	2842	2966	3145	3342	3355	4655	4838	0.5256012	0.5049217
47	463344.1	5804738	0.84	6.2	4.0	65.98	0.1374998	401.30888	1125.6015	6.790218	1902	2206	2672	2872	2998	3164	3370	3394	4764	4888	0.4946183	0.4862506
48	463369.1	5804781	1.02	5.7	2.8	64.31	0.1162510	185.42679	1186.9914	6.680550	1924	2202	2618	2820	2952	3099	3332	3361	4589	4647	0.5504202	0.5277070
49	463344.1	5804824	0.77	5.7	4.9	63.60	0.1412506	254.36738	1154.7875	6.546160	1946	2190	2634	2867	2983	3142	3366	3406	4763	4876	0.5212557	0.5052580
50	463369.1	5804868	1.12	6.4	3.7	61.62	0.1587496	215.01121	1229.1417	6.606883	1939	2190	2624	2819	2928	3096	3364	3316	4650	4777	0.5443661	0.5196901
51	463344.1	5804911	1.01	6.7	4.8	60.06	0.1624999	285.99590	1270.4820	6.713407	1880	2104	2514	2562	2700	2851	3188	3058	4279	4325	0.5854939	0.5507156
52	463369.1	5804954	1.78	7.4	12.6	58.70	0.1225004	68.16069	1438.2642	7.048402	1737	1878	2142	2241	2362	2518	2726	2728	3781	3702	0.6663910	0.6153949
53	463344.1	5804997	1.61	7.2	10.5	58.53	0.0574999	79.78436	1489.6332	7.271537	1625	1796	2060	2262	2357	2500	2684	2722	3804	3803	0.6436129	0.6008962
54	463362.6	5805028	1.98	7.3	10.7	57.87	0.1137505	61.61947	1491.7545	7.377023	1574	1692	1926	2102	2205	2347	2560	2591	3868	3838	0.6615038	0.6076294
55	463337.6	5805071	1.96	7.4	8.7	57.89	0.0350003	70.41354	1304.4460	7.353888	1666	1827	2112	2294	2405	2576	2760	2826	3971	3963	0.6580003	0.6131830
56	463362.6	5805115	1.51	7.4	11.4	58.04	0.0937495	57.27010	1380.2259	7.211137	1643	1758	2028	2300	2404	2526	2650	2791	4078	4046	0.6408364	0.6074710
57	463337.6	5805158	1.26	6.9	12.1	58.97	0.1087489	75.33991	1327.4143	7.018883	1651	1862	2176	2242	2338	2523	2824	2760	4050	4018	0.5939948	0.5519542
58	463362.6	5805201	1.02	6.1	6.1	59.01	0.0387516	182.08780	1259.4245	6.805560	1836	2062	2404	2694	2838	3009	3216	3253	4591	4673	0.5250132	0.5093815
59	463337.6	5805244	1.15	6.4	6.6	59.19	0.0274992	187.69984	1370.8010	6.825978	1844	2088	2480	2840	2930	3185	3304	3418	4595	4624	0.5678887	0.5350615
60	463362.6	5805288	0.91	6.4	7.1	60.26	0.0874996	159.41856	1401.7567	6.817807	1969	2246	2722	2900	3036	3206	3452	3397	4539	4590	0.5227429	0.5069054
61	463337.6	5805331	0.97	6.3	6.7	59.97	0.0924988	248.06975	1371.9776	6.837788	1972	2246	2706	2839	3528	3756	3552	3974	3985	3801	0.5330487	0.5141700
62	463362.6	5805374	0.8	6.5	6.3	59.63	0.0899997	314.88365	1377.6456	6.785805	2016	2302	2758	3010	3209	3371	3604	3623	4668	4720	0.4768166	0.4780952
63	463394.1	5804564	0.83	6.1	3.3	70.63	0.2424984	497.93137	969.5480	6.796362	1868	2218	2694	2989	3116	3288	3496	3473	4610	4618	0.3595028	0.3734303
64	463419.1	5804608	0.8	6.3	6.6	71.17	0.3787508	117.75316	1194.7171	6.827658	1973	2244	2710	2920	3024	3187	3476	3391	4492	4514	0.4887417	0.4668842
65	463394.1	5804651	0.65	6.0	2.6	68.78	0.2399998	488.78637	1049.0889	6.799809	1944	2248	2704	2962	3102	3287	3510	3450	4744	4866	0.4501101	0.4381720
66	463419.1	5804694	0.84	5.9	5.3	66.97	0.0974989	280.66584	1109.4204	6.805694	1914	2208	2648	2864	2988	3164	3382	3386	4608	4668	0.5448635	0.5169992
67	463394.1	5804738	0.98	6.3	3.8	65.35	0.1250000	310.02624	1172.2114	6.780546	1930	2188	2628	2824	2956	3090	3308	3319	4566	4654	0.5606304	0.5325332
68	463419.1	5804781	1.1	6.3	8.0	63.72	0.1825008	121.17439	1244.2248	6.752487	1928	2248	2656	2846	2957	3128	3348	3354	4550	4576	0.5840203	0.5527584
69	463394.1	5804824	0.9	5.5	3.9	62.86	0.1137495	282.68969	1204.1554	6.611118	1954	2194	2676	2889	3001	3143	3398	3396	4661	4776	0.5891755	0.5561754
70	463419.1	5804868	0.97	6.4	8.1	61.15	0.1687493	115.83539	1229.2918	6.793893	1928	2180	2624	2790	2910	3071	3326	3298	4445	4580	0.5312449	0.5060494
71	463394.1	5804911	1.01	6.4	4.4	59.69	0.1249995	200.21414	1321.7875	6.863470	1881	2052	2414	2392	2522	2667	3030	2878	3853	3836	0.5855856	0.5479818
72	463419.1	5804954	1.78	7.1	9.0	58.26	0.0762501	69.07130	1256.0558	7.136433	1656	1794	2066	2151	2261	2424	2726	2649	3819	3796	0.6773406	0.6257233
73	463387.6	5804985	1.82	7.1	11.0	58.07	0.0437498	62.64422	1410.7650	7.221829	1616	1772	2060	2199	2298	2435	2678	2664	3875	3826	0.6537082	0.6031150
74	463412.6	5805028	3.16	7.4	12.3	57.41	0.0224996	55.93398	1335.1514	7.353502	1576	1730	1950	2124	2228	2371	2542	2579	3878	3852	0.6691604	0.6224078
75	463387.6	5805071	2.72	7.4	14.8	57.51	0.0099988	54.78349	1394.9452	7.339515	1615	1735	1972	2131	2226	2380	2572	2627	3906	3878	0.6640812	0.6133443
76	463412.6	5805115	1.41	6.8	10.6	58.19	0.0950003	81.97400	1359.5303	7.050184	1672	1820	2098	2344	2477	2625	2778	2896	4191	4133	0.6506461	0.6056497
77	463387.6	5805158	1.06	6.0	8.0	59.03	0.0412493	103.70253	1357.2603	6.886902	1719	1924	2254	2405	2511	2702	2974	2916	4194	4129	0.5886691	0.5593945
78	463412.6	5805201	0.89	5.8	7.8	59.00	0.1450000	110.20900	1417.1538	6.650871	1834	2112	2510	2740	2861	2991	3254	3236	4545	4519	0.5240055	0.5095109
79	463387.6	5805244	0.91	6.0	5.8	59.94	0.0662503	277.15511	1265.7415	6.730685	1954	2252	2710	2966	3076	3259	3452	3489	4685	4781	0.4583990	0.4589101
80	463412.6	5805288	0.73	6.3	3.5	60.30	0.0599999	190.40388	1358.1637	6.787226	1966	2290	2750	2990	3127	3282	3484	3537	4689	4790	0.5134113	0.4994889
81	463387.6	5805331	0.79	6.6	4.5	60.05	0.1250010	414.78232	1375.3063	6.825928	2023	2356	2818	3044	3162	3353	3640	3551	4726	4817	0.5267903	0.5146811
82	463412.6	5805374	0.8	5.9	11.9	59.64	0.1062498	267.93243	1426.9886	6.752378	2009	2330	2792	3026	3171	3325	3578	3542	4633	4721	0.5091774	0.4957049
83	463444.1	5804564	0.63	6.6	3.9	69.94	0.2375002	693.72278	790.6023	6.880600	1856	2228	2702	2789	2939	3100	3396	3276	4420	4332	0.3064516	0.3353116
84	463469.1	5804608	0.72	6.7	3.1	68.14	0.2687492	446.62110	1036.8473	6.864885	1955	2270	2710	2795	2935	3091	3424	3261	4467	4447	0.4873634	0.4767718
85	463444.1	5804651	0.8	5.8	4.6	67.93	0.0824995	461.87865	1088.2814	6.819734	1987	2290	2750	3028	3169	3331	3544	3555	4757	4874	0.5227989	0.4972286
86	463469.1	5804694	0.89	5.8	6.1	67.17	0.0912495	83.89641	1222.5409	6.750419	1920	2214	2630	2858	2983	3149	3374	3376	4457	4470	0.5952897	0.5628415
87	463444.1	5804738	1.01	6.2	7.1	65.45	0.1587515	88.16160	1217.7181	6.750646	1929	2196	2628	2821	2937	3078	3344	3316	4460	4448	0.6086287	0.5685096
88	463469.1	5804781	0.94	6.0	5.5	63.12	0.1624999	158.48519	1173.9261	6.773363	1893	2124	2590	2786	2905	3077	3310	3304	4532	4544	0.5837260	0.5489322
89	463444.1	5804824	0.99	6.3	5.0	62.08	0.1100011	144.35661	1219.6687	6.795249	1924	2190	2608	2822	2947	3100	3342	3347	4618	4685	0.5960347	0.5616854
90	463469.1	5804868	1.27	6.8	5.7	60.52	0.1174994	128.52191	1232.0866	7.048964	1834	2022	2394	2568	2680	2808	3016	3014	3983	4036	0.6277761	0.5818705
91	463444.1	5804911	1.48	6.8	6.1	59.04	0.1537499	129.81597	1289.6311	7.117906	1792	1988	2300	2406	2520	2668	2824	2872	3884	3927	0.5858179	0.5505830
92	463469.1	5804932	1.6	7.3	6.2	58.03	0.1187506	65.02794	1187.1534	7.287864	1688	1868	2156	2319	2431	2544	2806	2798	3961	4025	0.6657534	0.6148738
93	463417.3	5804987	2.42	7.3	12.9	57.72	0.0775003	45.48428	1393.0189	7.259055	1574	1716	1956	2100	2207	2366	2550	2598	3754	3732	0.6682779	0.6197372
94	463462.6	5805044	2.82	7.4	10.1	57.23	0.0350008	39.59307	1326.4870	7.370984	1752	1878	2232	2202	2251	2414	2820	2615	3877	3931	0.6623121	0.6162251
95	463437.6	5805071	3.13	7.5	16.2	57.32	0.0387502	65.77803	1284.1161	7.291442	1602	1744	1974	2128	2218	2354	2512	2579	3930	3939	0.6695652	0.6197108
96	463462.6	5805115	1.63	7.2	8.8	57.86	0.1349998	76.05850	1438.9688	7.016274	1644	1766	2054	2263	2370	2542	2652	2781	4077	4050	0.6462684	0.6073007
97	463437.6	5805158	1.33	5.8	6.6	58.82	0.0687499	129.72247	1366.4189	6.745273	1726	1916	2260	2401	2511	2665	2986	2922	4243	4158	0.6071772	0.5662763
98	463462.6	5805201	1.23	5.8	7.0	59.04	0.1162496	142.07825	1461.1715	6.580373	1796	2030	2408	2595	2733	2900	3108	3127	4378	4332	0.5482158	0.5256788
99	463437.6	5805244	1.17	6.4	7.5	60.15	0.0337505	87.56203	1563.9678	6.626196	1904	2192	2620	2986	3085	3263	3366	3462	4734	4769	0.5155875	0.5055300
100	463462.6	5805288	0.95	6.1	6.2	60.02	0.0462499	164.06361	1444.5413	6.692768	1928	2190	2654	2980	3094	3285	3350	3530	4709	4720	0.5474524	0.5229093
101	463437.6	5805331	0.72	6.0	4.5	60.28	0.0312490	131.56674	1477.0884	6.759448	1922	2236	2676	3005	3140	3274	3390	3484	4600	4649	0.5203745	0.5008559
102	463462.6	5805374	0.89	6.0	4.5	60.10	0.0712495	328.48193	1415.5441	6.687316	1996	2320	2804	2981	3121	3313	3590	3559	4668	4753	0.5441892	0.5310941
103	463494.1	5804651	0.87	6.0	5.1	67.55	0.0337477	125.10376	1138.8122	6.788760	1908	2162	2538	2824	2908	3082	3258	3263	4391	4428	0.5855624	0.5418364
104	463519.1	5804694	0.9	6.1	4.9	66.49	0.1162491	263.16166	1130.7420	6.720321	1930	2180	2592	2800	2909	3065	3276	3261	4310	4274	0.5688838	0.5308563
105	463494.1	5804738	0.91	6.5	5.2	65.04	0.2012501	159.35400	1179.1147	6.731754	1958	2224	2622	2829	2958	3115	3334	3357	4518	4493	0.5913910	0.5513730
106	463519.1	5804781	0.74	6.3	5.0	62.59	0.1512494	388.40984	1129.6663	6.820396	1894	2146	2542	2854	3007	3135	3276	3333	4617	4715	0.6097561	0.5671233
107	463494.1	5804824	0.95	6.9	7.7	61.52	0.1362495	249.10863	1185.4905	6.937549	1884	2104	2490	2729	2832	2960	3230	3245	4431	4531	0.5717916	0.5435969
108	463519.1	5804868	1.48	7.2	3.3	59.90	0.1762495	93.90455	1222.2550	7.175188	1791	1982	2334	2366	2481	2611	2904	2854	3893	3902	0.6359577	0.5884393
109	463494.1	5804911	1.4	7.0	5.4	58.50	0.1287494	104.08597	1224.0041	7.300752	1725	1897	2198	2343	2462	2615	2838	2872	4016	4029	0.6406661	0.5909348
110	463512.6	5804941	2.34	7.4	7.6	57.65	0.0449996	36.95679	1124.7133	7.394449	1643	1762	1994	2299	2303	2547	2596	2748	3967	4032	0.6650691	0.6016860
111	463489.0	5804998	1.79	7.3	8.6	57.44	0.0787501	44.72649	1237.2641	7.441678	1676	1857	2062	2197	2960	2945	2768	3244	3723	3454	0.6161240	0.5665765
112	463512.6	5805028	2.27	7.4	15.9	57.24	0.0499988	71.00161	1232.1745	7.448153	1674	1845	2102	2228	2467	2524	2676	2790	3926	3856	0.6574477	0.6023344
113	463487.6	5805071	2.81	7.4	16.1	57.24	0.0249996	59.92226	1249.1956	7.288977	1678	1827	2090	2150	2240	2338	2646	2566	3891	3938	0.6739247	0.6230940
114	463512.6	5805115	1.56	6.9	6.2	57.82	0.0612507	96.26552	1284.8643	7.056897	1637	1796	2036	2362	2458	2594	2660	2829	4156	4171	0.6309851	0.5885935
115	463487.6	5805158	1.11	6.0	6.8	58.56	0.0512495	122.26806	1364.1095	6.722092	1788	2010	2388	2451	2565	2723	3058	2955	4225	4193	0.5750328	0.5491460
116	463512.6	5805201	0.87	5.8	6.9	59.01	0.0912514	179.68730	1377.5330	6.549329	1864	2152	2590	2734	2841	2993	3276	3224	4479	4458	0.5441370	0.5173976
117	463487.6	5805244	0.92	5.9	7.0	59.80	0.0462494	176.82521	1438.6507	6.603609	1910	2176	2612	2834	2984	3136	3356	3386	4608	4648	0.5553743	0.5311496
118	463512.6	5805288	0.82	6.1	6.6	60.47	0.0487509	114.49289	1429.7880	6.631100	1948	2218	2672	2936	3034	3238	3388	3440	4610	4656	0.5761737	0.5465371
119	463487.6	5805331	0.86	6.0	6.0	60.44	0.0762515	212.90986	1384.9897	6.675665	1978	2270	2712	3003	3127	3308	3490	3494	4669	4697	0.5498877	0.5244557
120	463512.6	5805374	1	6.3	6.3	60.75	0.0925002	264.73054	1290.1573	6.655729	1928	2216	2636	2910	3055	3269	3354	3428	4612	4686	0.5771737	0.5471698
121	463544.1	5804824	1.23	7.1	6.4	61.19	0.0937505	161.83044	1144.5785	6.984307	1872	2038	2350	2461	2558	2811	3042	2916	3794	3767	0.6463626	0.5961377
122	463569.1	5804868	1.41	7.3	5.2	59.77	0.1450000	135.44327	1145.5539	7.131771	1718	1892	2172	2381	2507	2640	2830	2864	4033	4040	0.6824832	0.6092074
123	463544.1	5804911	1.59	7.2	12.0	58.33	0.1050005	57.93237	1163.7498	7.332167	1657	1796	2028	2137	2269	2411	2710	2649	3836	3754	0.6700374	0.6191244
124	463562.6	5804941	2.49	7.4	7.0	57.56	0.0412502	48.52231	1203.2409	7.379164	1596	1744	1948	2080	2207	2333	2508	2547	3791	3739	0.6834040	0.6208668
125	463537.6	5804985	3.06	7.5	10.2	57.43	0.0200009	55.93960	1132.1643	7.456781	1602	1730	1960	2184	2254	2412	2522	2626	3926	3963	0.6614045	0.5991616
126	463562.6	5805028	2.53	7.5	12.6	57.16	0.0437508	62.03869	1234.1593	7.403219	1602	1718	1936	2096	2162	2286	2532	2527	3803	3801	0.6568448	0.5934915
127	463537.6	5805071	1.72	7.2	7.4	57.70	0.1524997	72.74217	1262.3662	7.313991	1620	1767	2046	2090	2237	2360	2632	2593	3997	4065	0.6041032	0.5596073
128	463562.6	5805115	1.21	6.3	5.4	57.85	0.1100011	127.33624	1267.9595	7.067966	1756	1948	2248	2605	2729	2864	2930	3117	4424	4448	0.6053375	0.5633695
129	463537.6	5805158	1	6.0	6.6	58.34	0.0624995	232.64720	1301.7935	6.787254	1830	2064	2440	2545	2637	2824	3166	3076	4309	4329	0.5712435	0.5442393
130	463562.6	5805201	0.87	6.1	5.4	59.29	0.0924997	323.03271	1287.0772	6.638816	1874	2170	2642	2869	2986	3128	3384	3372	4676	4738	0.5654849	0.5405448
131	463537.6	5805244	0.95	5.8	4.6	59.87	0.0650005	187.02540	1300.4915	6.567674	1920	2236	2700	2907	3025	3182	3386	3418	4587	4653	0.5629820	0.5380237
132	463562.6	5805288	0.77	5.9	2.3	61.60	0.1137495	323.09171	1119.8698	6.610454	2013	2288	2782	3012	3150	3298	3552	3535	4778	4861	0.4746483	0.4636364
133	463537.6	5805331	0.92	6.1	8.3	61.34	0.2087493	159.67189	1298.6889	6.627419	1922	2184	2638	2909	2996	3197	3354	3381	4547	4578	0.6063862	0.5744809
134	463562.6	5805374	0.8	6.2	6.4	61.89	0.1949997	388.71387	1143.0183	6.661456	1954	2250	2694	2893	3049	3235	3426	3435	4598	4727	0.4452994	0.4400000
135	463587.6	5804898	1.03	6.3	6.3	58.86	0.1275001	130.20053	1182.4615	7.169967	1705	1874	2152	2368	2496	2676	2820	2894	4027	3998	0.6456799	0.5932499
136	463601.8	5804947	1.49	6.8	6.5	57.81	0.0124998	118.99471	1186.0694	7.206483	1610	1754	1946	2210	2324	2488	2620	2710	4011	4017	0.6637347	0.6067400
137	463587.6	5804985	2.21	7.2	7.1	57.64	0.0275002	69.43207	1208.4539	7.318411	1567	1692	1890	2045	2201	2317	2476	2503	3753	3782	0.6304878	0.5759540
138	463612.6	5805028	1.78	6.8	7.2	57.52	0.0999994	133.76059	1239.0210	7.169884	1584	1694	1918	2059	2142	2270	2450	2482	3799	3853	0.6238058	0.5697199
139	463587.6	5805071	2.74	7.2	14.0	57.35	0.0437493	62.89901	1360.7079	7.182036	1651	1766	2042	2130	2267	2391	2636	2626	4027	4035	0.5850461	0.5494384
140	463612.6	5805115	1.2	6.6	7.5	57.97	0.0862498	158.15175	1270.1886	6.932949	1727	1874	2196	2523	2657	2777	2858	3046	4313	4350	0.5797460	0.5408623
141	463587.6	5805158	1.06	6.1	5.4	58.66	0.1200004	199.11154	1262.0122	6.801995	1872	2118	2550	2679	2808	2974	3286	3192	4471	4536	0.5549806	0.5316980
142	463612.6	5805201	0.8	5.8	4.9	59.93	0.1024990	315.44639	1252.1190	6.719218	1910	2186	2660	2887	3003	3158	3392	3396	4700	4784	0.5418904	0.5193972
143	463587.6	5805244	0.74	6.1	3.5	60.49	0.0912509	400.65960	1145.8750	6.642469	1950	2248	2702	2998	3115	3270	3454	3514	4868	5007	0.5440195	0.5207565
144	463612.6	5805288	0.52	6.3	3.2	62.12	0.0587506	494.78533	1035.8148	6.716818	1990	2296	2762	2955	3065	3245	3530	3464	4794	4970	0.4337662	0.4370322
145	463587.6	5805331	0.57	6.6	1.8	63.16	0.0512495	255.23615	1114.6776	6.678369	1924	2262	2716	2955	3085	3227	3468	3446	4709	4857	0.4466897	0.4358389
146	463612.6	5805374	0.67	7.0	5.6	62.97	0.1850004	240.56692	1112.5206	6.754630	1932	2210	2628	2846	2981	3150	3382	3366	4571	4741	0.4262566	0.4260208
147	463637.6	5805071	1.27	6.3	6.5	57.47	0.0450001	197.79463	1207.0716	6.952288	1720	1878	2144	2177	2298	2446	2760	2682	4000	4027	0.5599865	0.5186708
148	463662.6	5805115	0.78	5.8	5.9	57.98	0.0949993	203.84794	1214.5487	6.766295	1816	2052	2448	2605	2689	2836	3074	3028	4203	4215	0.5374893	0.5061067
149	463637.6	5805158	0.91	6.6	6.6	59.32	0.1112509	117.61061	1306.8628	6.755830	1803	2042	2444	2660	2774	2923	3088	3187	4431	4453	0.5444780	0.5134868
150	463662.6	5805201	0.71	6.1	4.3	60.49	0.1062503	216.18767	1177.2206	6.756177	1943	2218	2628	2812	2928	3069	3312	3279	4547	4641	0.4857143	0.4660178
151	463637.6	5805244	0.85	6.5	3.0	61.23	0.0812502	421.01518	1180.4252	6.768052	1926	2220	2698	3053	3180	3325	3452	3609	4890	5055	0.5146526	0.4925373
152	463662.6	5805288	0.81	6.4	4.5	61.84	0.0949998	228.28751	1141.6795	6.851031	1946	2242	2672	2865	2975	3156	3398	3367	4673	4788	0.4838063	0.4676354
153	463637.6	5805331	0.73	6.3	3.0	61.19	0.1300006	422.32591	1038.5827	6.806584	1900	2186	2632	2914	3061	3183	3336	3442	4708	4868	0.4098637	0.4115268
154	463662.6	5805374	0.6	6.1	2.7	61.84	0.1037507	263.48489	1043.4323	6.850850	1956	2254	2704	2922	3039	3221	3502	3451	4706	4857	0.4569362	0.4441186
155	463661.3	5805067	0.85	6.1	5.3	57.71	0.0337501	199.82453	1148.7023	6.850561	1836	2001	2296	2436	2524	2660	2956	2926	4142	4197	0.4831304	0.4645372
156	463712.6	5805115	0.86	5.8	5.8	57.56	0.0937500	233.46077	1131.9118	6.643258	1846	2064	2454	2652	2754	2910	3070	3146	4315	4331	0.4985189	0.4802065
157	463687.6	5805158	0.84	6.3	5.0	58.89	0.1837497	234.13663	1159.0834	6.683413	1850	2118	2500	2645	2768	2916	3108	3098	4274	4279	0.4955203	0.4782016
158	463712.6	5805201	0.82	6.5	3.9	59.94	0.1662502	434.43134	1084.1440	6.727150	1916	2216	2620	2797	2933	3053	3268	3257	4457	4531	0.4848588	0.4673840
159	463687.6	5805244	0.78	6.1	2.5	61.98	0.0887504	234.28404	1101.4893	6.818412	1927	2222	2684	2887	2963	3174	3348	3303	4531	4622	0.4540278	0.4491738
160	463712.6	5805288	0.59	6.5	3.3	61.34	0.0874996	358.83170	1093.8935	6.866570	1952	2216	2650	2739	2804	3014	3324	3219	4382	4507	0.4354644	0.4181137
161	463687.6	5805331	0.84	6.6	4.4	60.36	0.1012502	394.30945	1064.9895	6.883670	1875	2172	2594	2806	2939	3086	3316	3305	4601	4760	0.4674715	0.4456558
162	463712.6	5805374	0.57	5.9	2.5	60.61	0.0937500	464.05772	1034.1321	6.868661	1938	2266	2696	2926	3046	3252	3470	3419	4685	4853	0.3947020	0.4021305
163	463214.6	5805009	1.02	6.5	7.5	60.38	0.0862503	246.55051	1344.9051	6.683669	1805	2019	2392	2581	2760	3115	3194	3379	4154	4226	0.5150461	0.5012065
164	463762.6	5805115	0.91	6.2	4.6	57.51	0.0900011	271.10841	1099.4354	6.623403	1839	2076	2462	2687	2801	2937	3060	3146	4329	4393	0.5072667	0.4815835
165	463737.6	5805158	0.83	6.2	4.8	59.11	0.1037498	284.24933	1128.1129	6.653250	1874	2094	2500	2684	2764	2913	3120	3092	4227	4255	0.5304107	0.5081967
166	463762.6	5805201	0.79	6.0	2.9	59.32	0.0474992	489.42159	1081.3981	6.734506	1928	2150	2554	2781	2860	3019	3232	3244	4430	4508	0.5031469	0.4780815
167	463737.6	5805244	0.8	6.4	7.7	61.55	0.2562499	156.14031	1101.8771	6.797244	1932	2262	2688	2831	2949	3054	3316	3300	4385	4431	0.4762221	0.4667107
168	463762.6	5805288	0.7	6.1	3.8	61.23	0.1537499	248.96839	1161.4840	6.763531	1914	2166	2584	2822	2917	3056	3226	3282	4418	4500	0.4643466	0.4514711
169	463737.6	5805331	0.57	6.2	2.9	60.03	0.0774999	513.36578	1068.1898	6.825418	1888	2182	2636	2773	2879	3028	3300	3252	4454	4597	0.4555404	0.4520641
170	463762.6	5805374	0.54	6.4	1.8	59.69	0.0387497	335.20815	1077.0669	6.730819	1949	2266	2672	2871	2971	3158	3420	3358	4487	4545	0.4678432	0.4540259
171	463787.6	5805158	0.68	6.1	2.7	59.36	0.0812492	336.53319	1051.3261	6.687310	1886	2144	2526	2754	2839	3013	3178	3201	4421	4480	0.4453379	0.4450907
172	463812.6	5805201	0.98	6.0	6.1	58.78	0.0875006	508.59832	1044.9392	6.741808	1893	2144	2534	2759	2828	3004	3158	3190	4367	4461	0.4272517	0.4297918
173	463787.6	5805244	0.76	6.5	4.5	60.20	0.0937500	443.54071	1051.5430	6.727672	1902	2224	2660	2734	2818	2954	3280	3141	4276	4366	0.4222820	0.4306964
174	463812.6	5805288	0.75	6.0	3.9	59.38	0.1324997	480.40858	1083.8094	6.651502	1892	2172	2560	2856	2950	3069	3244	3329	4460	4528	0.4269231	0.4192314
175	463787.6	5805331	0.75	5.2	2.8	59.25	0.0974994	469.55138	1104.1070	6.667091	1938	2186	2608	2840	2949	3119	3316	3337	4466	4539	0.5093039	0.4923339
176	463812.6	5805374	0.69	5.8	4.3	59.31	0.0162487	308.27369	1176.2606	6.552788	1980	2284	2716	2878	3038	3203	3448	3412	4477	4495	0.4900585	0.4772238
177	463837.6	5805158	0.86	6.2	3.5	59.03	0.0350003	261.23927	1040.4570	6.757152	1905	2194	2572	2782	2884	3024	3218	3233	4444	4550	0.4503817	0.4398898
178	463862.6	5805201	0.96	6.4	4.2	58.71	0.0275002	594.50480	1059.8442	6.799743	1907	2164	2540	2761	2855	3024	3126	3215	4442	4556	0.4773419	0.4598230
179	463837.6	5805244	0.57	6.6	3.4	59.99	0.0925007	304.30478	991.2611	6.695878	1912	2186	2632	2779	2866	3023	3266	3226	4414	4488	0.4170404	0.4141136
180	463862.6	5805288	0.87	6.0	4.6	58.43	0.0500002	582.55978	1092.2574	6.618117	1886	2166	2566	2810	2925	3051	3210	3270	4395	4464	0.4740363	0.4624520
181	463837.6	5805331	0.88	5.1	3.4	58.72	0.0487509	560.52120	1094.3056	6.525579	1926	2204	2606	2841	2950	3112	3370	3331	4455	4523	0.5202312	0.4953177
182	463862.6	5805374	0.73	5.3	3.0	59.44	0.0550008	400.98755	1116.1966	6.458205	1983	2274	2688	2904	3058	3205	3448	3417	4454	4519	0.4677447	0.4535446
183	464238.1	5805176	0.77	6.3	4.4	60.97	0.1550012	204.29248	1042.4866	6.814159	1963	2250	2688	2779	2901	3056	3410	3237	4467	4567	0.3773987	0.3959441
184	463928.9	5805104	0.98	5.8	3.7	59.63	0.0524998	366.22933	978.3690	6.716652	1848	2072	2452	2700	2802	2965	3074	3155	4418	4494	0.4194360	0.4098127
185	463887.6	5805158	0.85	6.4	4.5	59.89	0.1762505	174.90659	1071.5878	6.791008	1896	2154	2560	2767	2912	3072	3134	3293	4366	4433	0.4051578	0.4154845
186	463912.6	5805201	1	6.2	4.0	59.73	0.1174998	338.95689	983.0554	6.814855	1897	2206	2592	2793	2908	3047	3288	3298	4437	4559	0.4053590	0.4082616
187	463887.6	5805244	0.73	6.4	3.7	59.63	0.1075006	394.53528	1010.8559	6.766841	1952	2210	2632	2786	2884	3040	3226	3246	4358	4461	0.4038594	0.4082268
188	463912.6	5805288	0.83	6.4	4.2	58.64	0.1037502	373.41155	1033.7985	6.662338	1878	2164	2550	2852	2983	3120	3188	3294	4408	4542	0.4498607	0.4358621
189	463887.6	5805331	0.74	5.3	2.1	58.83	0.1925011	515.52662	1058.4789	6.517938	1956	2224	2708	2829	2904	3058	3448	3318	4420	4503	0.4638254	0.4643287
190	463912.6	5805374	0.83	6.1	3.9	60.22	0.0887499	142.73193	1155.0911	6.483220	1917	2224	2628	2851	2982	3122	3340	3314	4303	4393	0.4372598	0.4291411
191	463975.3	5805031	0.77	7.0	4.9	58.51	0.2012501	252.30026	1026.4099	6.688603	1854	2084	2458	2651	2789	2927	3062	3100	4292	4374	0.4170821	0.4166113
192	463937.6	5805064	0.95	5.8	4.1	59.27	0.0937505	245.97847	1021.4856	6.698418	1822	2044	2456	2614	2740	2894	3100	3086	4278	4312	0.4251285	0.4251285
193	463962.6	5805115	0.83	6.2	3.1	59.33	0.2399988	345.63455	991.9399	6.695840	1855	2080	2488	2702	2843	2962	3088	3177	4393	4481	0.4190828	0.4168421
194	463937.6	5805158	0.86	5.9	4.4	60.73	0.1349993	400.43720	978.7504	6.769126	1925	2156	2562	2787	2846	3019	3214	3207	4408	4512	0.4299279	0.4296765
195	463962.6	5805201	0.83	6.2	5.2	60.76	0.0437503	275.97630	1015.8449	6.786711	1921	2202	2610	2795	2875	3034	3256	3207	4408	4469	0.4108081	0.4148828
196	463937.6	5805244	0.72	5.9	3.4	60.81	0.0475011	357.05976	976.2837	6.792520	1896	2194	2598	2761	2886	3011	3190	3193	4384	4493	0.3981107	0.3924731
197	463962.6	5805288	0.88	6.5	5.1	58.84	0.0587506	343.48586	1044.3695	6.713204	1946	2234	2632	2904	3014	3167	3316	3383	4533	4585	0.4737756	0.4588276
198	463937.6	5805331	0.7	5.8	4.4	59.58	0.1212497	327.93896	1102.7830	6.578186	2008	2304	2738	2933	3075	3192	3422	3371	4494	4573	0.4738929	0.4599018
199	463962.6	5805374	0.72	6.2	3.9	58.84	0.1487503	257.03497	1188.7334	6.556452	1964	2276	2684	2916	3041	3187	3398	3409	4393	4450	0.5341923	0.5164082
200	464034.3	5805004	0.81	6.0	2.9	56.99	0.1774998	424.93683	990.0257	6.715249	1847	2068	2482	2646	2745	2942	3164	3139	4384	4441	0.4824713	0.4613358
201	464019.1	5805041	0.77	5.6	1.2	56.87	0.1762495	417.96169	991.0215	6.679208	1842	2096	2474	2635	2725	2900	3126	3099	4305	4406	0.4539204	0.4411812
202	463987.6	5805071	0.91	6.3	2.7	57.13	0.1562490	360.01053	1010.8574	6.664298	1830	2086	2472	2641	2743	2905	3108	3103	4343	4446	0.4460271	0.4281356
203	464012.6	5805115	0.75	5.8	1.7	58.24	0.3374982	285.61343	970.9984	6.657176	1898	2166	2592	2790	2885	3020	3264	3221	4466	4587	0.4619094	0.4356061
204	463987.6	5805158	0.72	6.1	2.9	61.34	0.1050005	199.81694	1015.1021	6.700363	1864	2092	2478	2719	2828	2969	3132	3163	4368	4420	0.3934222	0.3909494
205	464012.6	5805201	0.8	6.0	3.6	60.50	0.0325003	342.64073	1000.2086	6.727779	1880	2136	2548	2699	2807	2941	3188	3133	4360	4409	0.4586218	0.4394013
206	463987.6	5805244	0.89	6.0	2.8	59.58	0.1787491	488.49277	977.7148	6.759600	1850	2116	2524	2744	2890	3009	3190	3223	4415	4473	0.4168421	0.4109015
207	464012.6	5805288	0.77	5.8	3.2	57.98	0.0737500	308.09603	1055.0146	6.742199	1884	2164	2572	2824	2937	3067	3242	3300	4459	4494	0.4545455	0.4445777
208	463987.6	5805331	0.77	6.2	4.2	57.81	0.1137490	479.51302	1102.3564	6.648838	1979	2260	2676	2907	3045	3162	3374	3385	4523	4621	0.5206280	0.4934383
209	464012.6	5805374	0.83	6.4	5.4	57.24	0.0562491	198.17961	1216.9202	6.596526	1950	2194	2622	2904	3028	3218	3364	3416	4428	4444	0.5384109	0.5115565
210	464089.2	5804977	0.8	6.1	1.3	56.20	0.2237501	327.88069	988.3234	6.778899	1880	2154	2516	2724	2841	2999	3176	3246	4394	4479	0.4527814	0.4425177
211	464068.0	5805009	1	5.8	3.4	55.76	0.2512498	551.46433	1000.5587	6.731104	1854	2128	2522	2721	2841	2979	3204	3203	4399	4492	0.4858803	0.4636783
212	464069.1	5805041	1.01	6.2	3.7	55.12	0.1337504	451.80082	980.9917	6.708382	1820	2080	2440	2630	2726	2882	3042	3099	4319	4427	0.4244018	0.4253693
213	464037.6	5805071	0.74	6.5	1.9	56.19	0.1412501	391.30796	996.7293	6.664606	1814	2072	2444	2679	2792	2914	3054	3166	4408	4521	0.4322217	0.4171729
214	464062.6	5805115	0.78	6.6	1.6	58.57	0.5174994	229.82101	1029.8847	6.668668	1876	2178	2608	2807	2867	3014	3304	3232	4452	4553	0.4528302	0.4303406
215	464037.6	5805158	0.83	6.1	4.2	61.40	0.1574998	288.43205	1026.8307	6.653582	1802	2078	2426	2750	2833	2977	3042	3174	4333	4413	0.4764222	0.4587962
216	464062.6	5805201	0.41	7.1	2.0	61.56	0.2199998	415.93423	938.3535	6.675773	1908	2216	2650	2781	2887	3032	3292	3234	4444	4538	0.4218009	0.4182162
217	464037.6	5805244	0.78	6.3	3.7	58.78	0.1275005	431.10081	996.9637	6.708865	1855	2128	2506	2730	2823	2966	3148	3202	4382	4424	0.4436484	0.4299065
218	464062.6	5805288	0.87	6.3	4.2	57.41	0.1050000	329.45758	1050.6372	6.665808	1882	2138	2578	2817	2914	3039	3220	3284	4424	4485	0.4761354	0.4587890
219	464037.6	5805331	1.13	6.2	5.4	57.00	0.0312495	385.17797	1149.2864	6.650809	1914	2170	2596	2790	2920	3072	3298	3302	4440	4444	0.5281809	0.4998344
220	464062.6	5805374	0.91	6.5	5.2	56.59	0.1274991	276.60510	1254.4428	6.594189	1933	2230	2642	2817	2984	3122	3376	3349	4429	4447	0.5592105	0.5206930
221	464118.0	5805009	1.12	6.0	3.5	54.46	0.0812497	426.90570	999.9900	6.786303	1824	2012	2382	2564	2707	2831	3054	3036	4182	4243	0.4788877	0.4534413
222	464119.1	5805041	1.13	6.4	3.4	54.62	0.1512504	272.63562	983.3468	6.768493	1814	2066	2428	2703	2783	2936	3058	3134	4359	4483	0.4162402	0.4135876
223	464087.6	5805071	0.74	6.3	3.5	56.50	0.4562502	277.89785	969.9704	6.707753	1844	2094	2458	2665	2807	2926	3120	3113	4366	4475	0.4104316	0.4149114
224	464112.6	5805115	0.74	6.3	1.9	60.34	0.2562499	282.40738	959.8622	6.718361	1850	2108	2510	2755	2843	2997	3162	3208	4462	4554	0.3819232	0.3997591
225	464087.6	5805158	0.75	6.9	4.4	62.57	0.1012492	356.51029	958.5397	6.666695	1869	2136	2532	2768	2851	3029	3134	3202	4385	4516	0.3868950	0.3972466
226	464112.6	5805201	0.85	6.4	4.0	60.60	0.3674994	291.23382	1000.4743	6.664922	1852	2104	2478	2639	2730	2886	3082	3093	4234	4284	0.4798511	0.4535050
227	464087.6	5805244	0.84	5.8	2.9	58.21	0.0787497	486.30881	985.0688	6.668058	1858	2114	2556	2735	2852	3001	3176	3216	4415	4496	0.4517863	0.4309754
228	464112.6	5805288	0.83	5.8	6.0	56.96	0.0062504	499.28811	1066.0815	6.629854	1888	2120	2538	2872	3000	3137	3264	3358	4534	4620	0.5245331	0.4975124
229	464087.6	5805331	0.77	6.3	3.3	56.86	0.0637503	170.04909	1157.8106	6.615912	1974	2266	2678	2890	2995	3161	3392	3379	4479	4503	0.5129534	0.4893210
230	464112.6	5805374	0.81	6.4	4.7	55.64	0.1637497	334.43002	1251.0390	6.611192	1975	2252	2710	2901	3071	3200	3464	3415	4527	4543	0.5616354	0.5255255
231	464158.8	5805050	1.5	6.3	4.3	54.51	0.1124997	314.95652	960.0629	6.810427	1791	2036	2408	2664	2781	2927	3042	3148	4353	4436	0.3883983	0.3971075
232	464144.1	5805084	0.79	6.4	5.3	57.71	0.4625006	251.66512	962.9398	6.775894	1918	2166	2604	2758	2899	3024	3266	3243	4509	4591	0.3787448	0.3986418
233	464162.6	5805115	0.88	6.6	3.7	59.29	0.4000001	271.05057	976.3329	6.777590	1879	2176	2598	2838	2924	3076	3272	3287	4502	4609	0.3638778	0.3859649
234	464137.6	5805158	0.73	6.1	3.8	62.55	0.2262506	405.15755	960.6414	6.706226	1884	2174	2568	2769	2875	2989	3242	3214	4397	4496	0.4119967	0.4159525
235	464162.6	5805201	0.65	6.3	4.6	60.03	0.1875005	354.17928	1035.1585	6.698100	1833	2072	2436	2642	2760	2898	3094	3055	4192	4305	0.4475643	0.4327808
236	464137.6	5805244	0.9	6.3	3.9	58.00	0.0825005	388.72864	1018.7238	6.645541	1838	2134	2520	2743	2846	3007	3164	3213	4377	4465	0.4618776	0.4416358
237	464162.6	5805288	0.76	5.9	4.6	57.30	0.0500002	350.80516	1049.7547	6.648909	1864	2134	2546	2833	2967	3121	3244	3308	4480	4547	0.4875160	0.4643138
238	464137.6	5805331	0.72	6.3	4.4	56.17	0.1375008	212.22940	1178.4769	6.630773	1938	2222	2662	2878	2984	3183	3402	3388	4532	4512	0.5114504	0.4882651
239	464162.6	5805374	0.81	6.3	3.7	54.83	0.2125006	308.91472	1221.4945	6.658026	1950	2230	2600	2851	3015	3200	3398	3412	4467	4432	0.5622607	0.5246637
240	464201.5	5805101	0.68	7.0	2.7	58.17	0.2700005	208.16758	1022.7004	6.848679	1867	2198	2596	2682	2781	2928	3278	3111	4275	4389	0.3705499	0.3856032
241	464222.7	5805137	0.82	6.6	3.5	58.59	0.1412501	314.00298	986.2434	6.838198	1826	2064	2462	2634	2728	2876	3094	3075	4226	4302	0.4196819	0.4137511
242	464187.6	5805158	0.84	6.4	4.5	60.26	0.2512507	320.40348	986.7638	6.766054	1808	2082	2442	2709	2805	2939	3068	3130	4276	4364	0.4121888	0.4155911
243	464212.6	5805201	0.72	7.1	3.6	60.86	0.1875000	217.42829	1042.2177	6.749089	1830	2086	2424	2615	2737	2857	3050	3036	4150	4224	0.4426685	0.4277854
244	464187.6	5805244	0.72	6.1	3.9	59.05	0.0599999	199.94842	1047.4144	6.686224	1885	2156	2528	2736	2841	3004	3182	3199	4331	4438	0.4497702	0.4473943
245	464212.6	5805288	0.61	5.9	4.6	57.15	0.0962486	423.06156	1054.0783	6.717050	1867	2128	2534	2800	2908	3106	3248	3322	4461	4538	0.4978723	0.4768436
246	464187.6	5805331	0.78	6.0	4.0	55.83	0.1250000	344.29574	1106.2357	6.684262	1946	2236	2646	2835	2954	3144	3370	3348	4441	4492	0.5449984	0.5078806
247	464212.6	5805374	0.82	6.4	5.2	53.99	0.2562499	329.43684	1228.8529	6.729391	1993	2252	2664	2875	3029	3178	3416	3408	4398	4437	0.5769871	0.5369633
248	464237.6	5805244	0.86	6.4	3.6	58.65	0.2174997	278.47450	1030.9561	6.759171	1870	2106	2490	2720	2812	2994	3156	3222	4330	4386	0.4136808	0.4064472
249	464237.6	5805331	0.82	5.7	4.6	55.27	0.1799998	265.54026	1130.9986	6.760402	1942	2210	2612	2824	2981	3126	3358	3336	4433	4449	0.5554524	0.5149141
250	463528.0	5804749	0.71	6.0	2.7	64.23	0.2837496	349.27214	1113.9435	6.742702	1950	2216	2648	2799	2909	3092	3364	3301	4475	4532	0.5102659	0.4833058

(Source of data: Schmidinger et al. (2025) “LimeSoDa: A Dataset Collection for Benchmarking of Machine Learning Regressors in Digital Soil Mapping”)

20.4.3 Build the regression tree

The model is fitted as follows:

# Example formula predicting soil organic carbon from some covariates
SOC_formula <- SOC_target ~ x_25833 + y_25833 + Altitude + Slope + 
                        ERa + G_Total_Counts + NDVI + GNDVI

rtree_soc_model <- rpart( 
    formula = SOC_formula, 
    data = BB.250, 
    method = "anova" 
)

20.4.4 Plot the tree

rpart.plot( rtree_soc_model, 
            type = 2, 
            fallen.leaves = TRUE, 
            extra = 101,
            main = "Regression Tree per SOC"
)

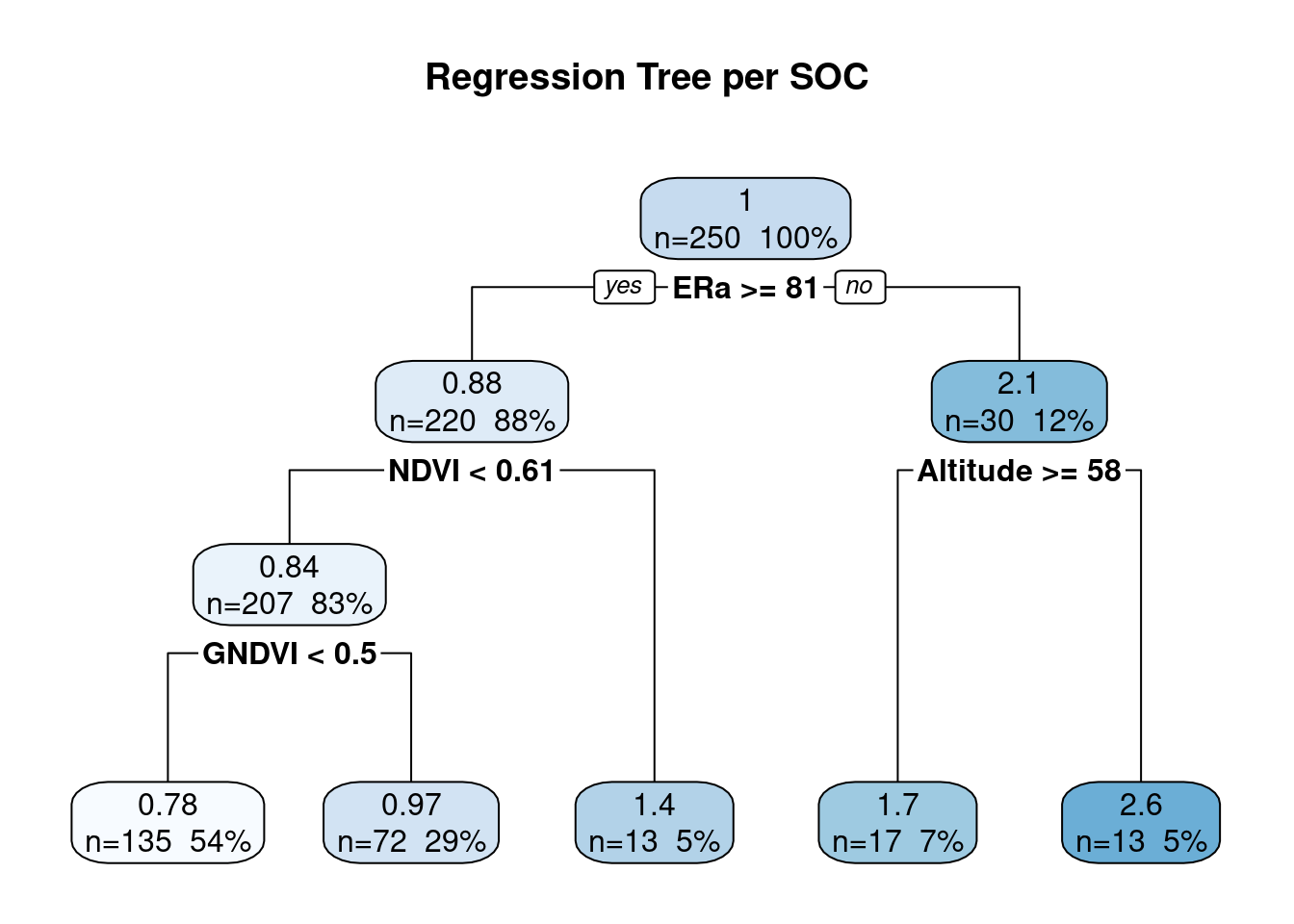
This produces a visual representation of the tree structure, showing the splitting rules at each node, the number of observations, and the predicted value in each leaf.

20.4.5 How to interpret the regression tree model

The regression tree divides the dataset into smaller groups based on a series of simple rules. Each rule is a question about one variable — for example:

“Is ERa (Apparent Electrical Resistivity) less than 80.88?”

At each step, the data is split into two branches, forming a “tree” structure where:

Each internal node contains a decision rule (called a split).
Each leaf node (or terminal node) provides a predicted value — the average of the SOC_target values within that group.

20.4.5.1 Example from the fitted model

The first split (at the top of the tree) is:

ERa < 80.88

This means ERa is the most important variable for predicting SOC — it creates the largest reduction in prediction error.

If a data point has ERa < 80.88, it goes to the right branch, where the average SOC is about 2.09.
Otherwise, it goes to the left branch, with a lower SOC average around 0.88.
From there, the tree continues to split the data further — based on NDVI, GNDVI, and Altitude — refining the prediction at each step.

20.4.5.2 Which variables matter most?

The model tells us which variables were most important:

# Normalize and plot variable importance
imp <- rtree_soc_model$variable.importance
imp_norm <- imp / sum(imp)

barplot(imp_norm,
        las = 2, col = "sienna",
        main = "Normalized Variable Importance",
        ylab = "Proportion")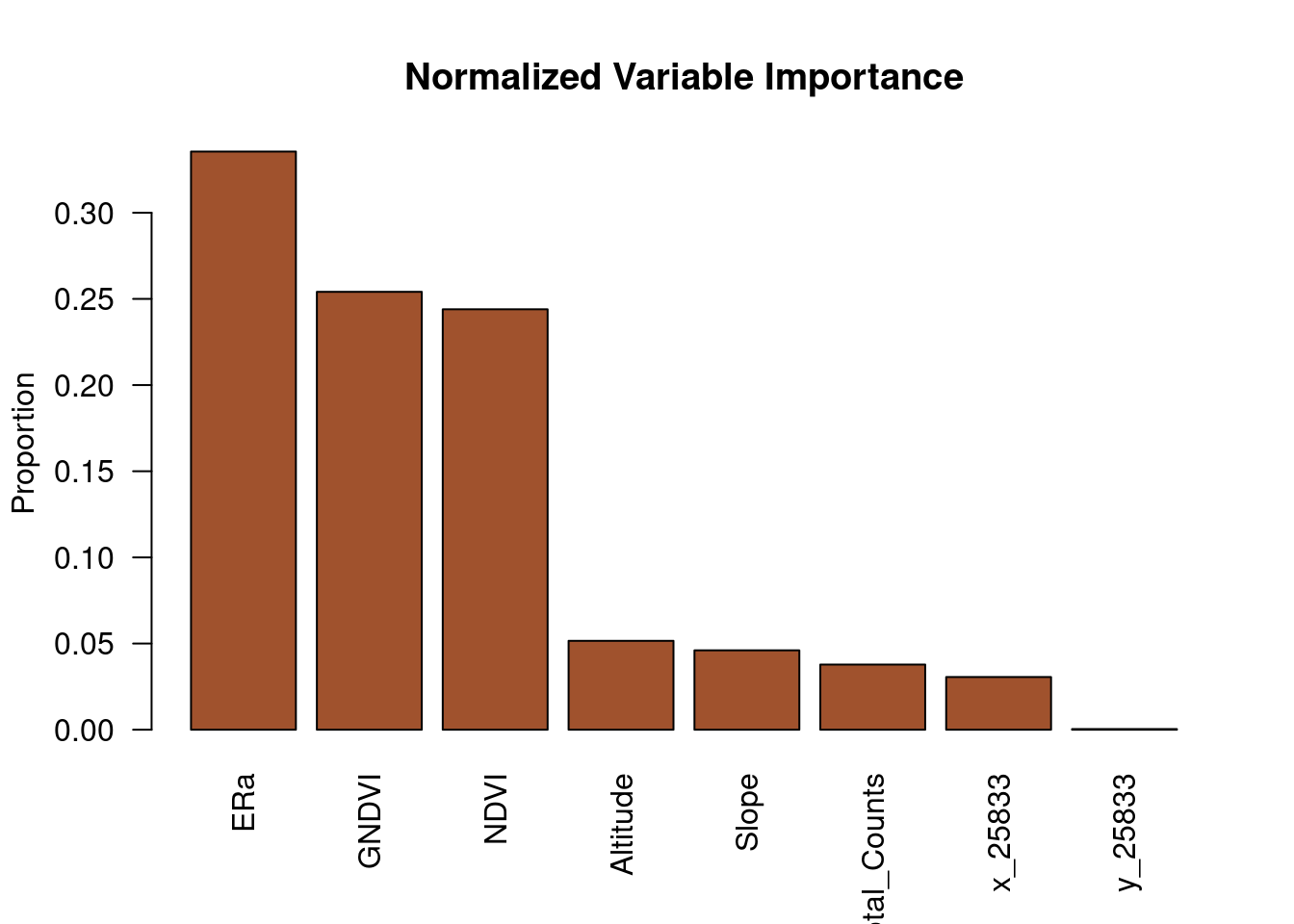

This means that soil electrical resistivity (ERa), vegetation indices (NDVI and GNDVI), and altitude are the most influential in predicting SOC.

20.4.6 Predict

20.4.6.1 Predict SOC using the regression tree

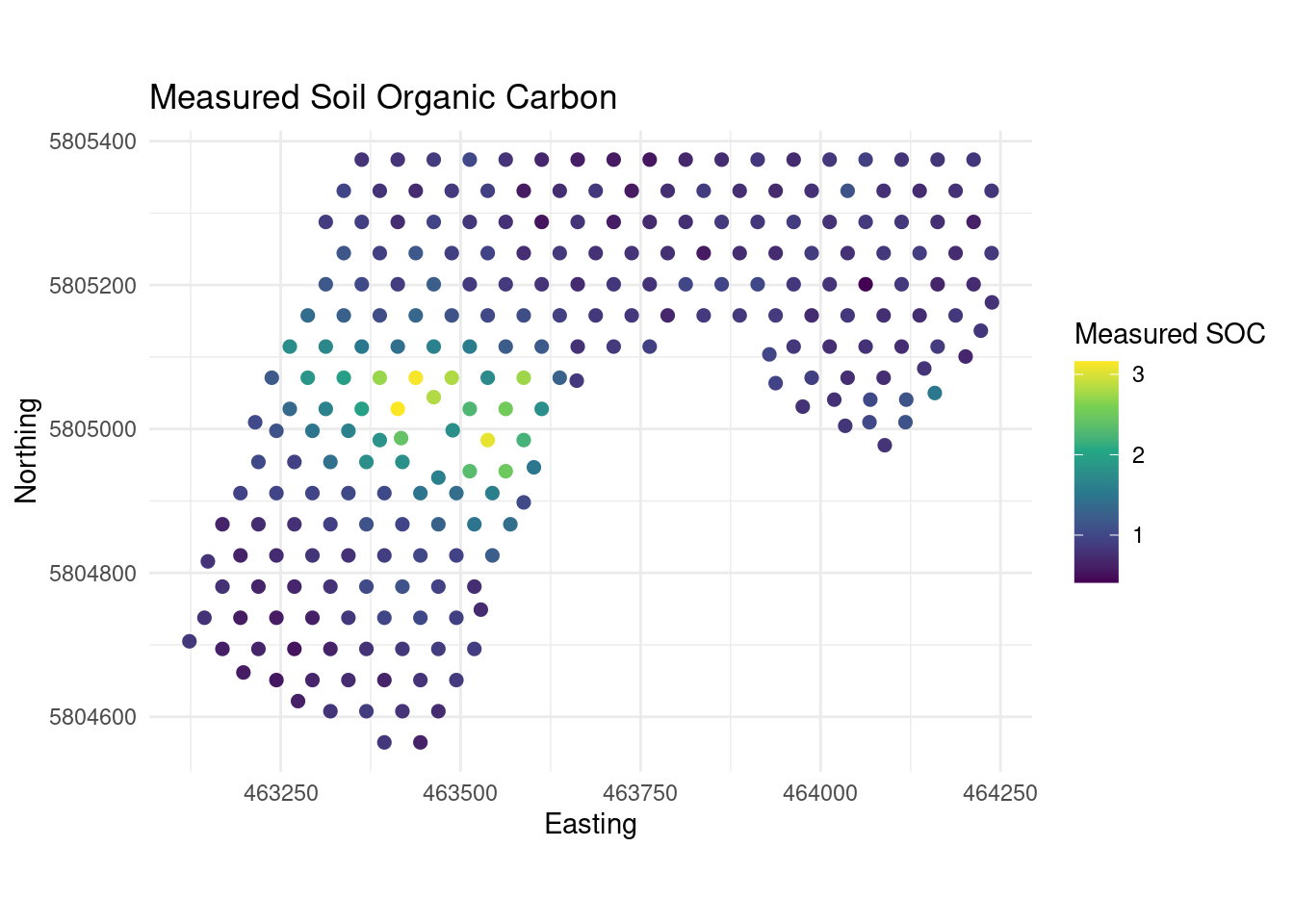
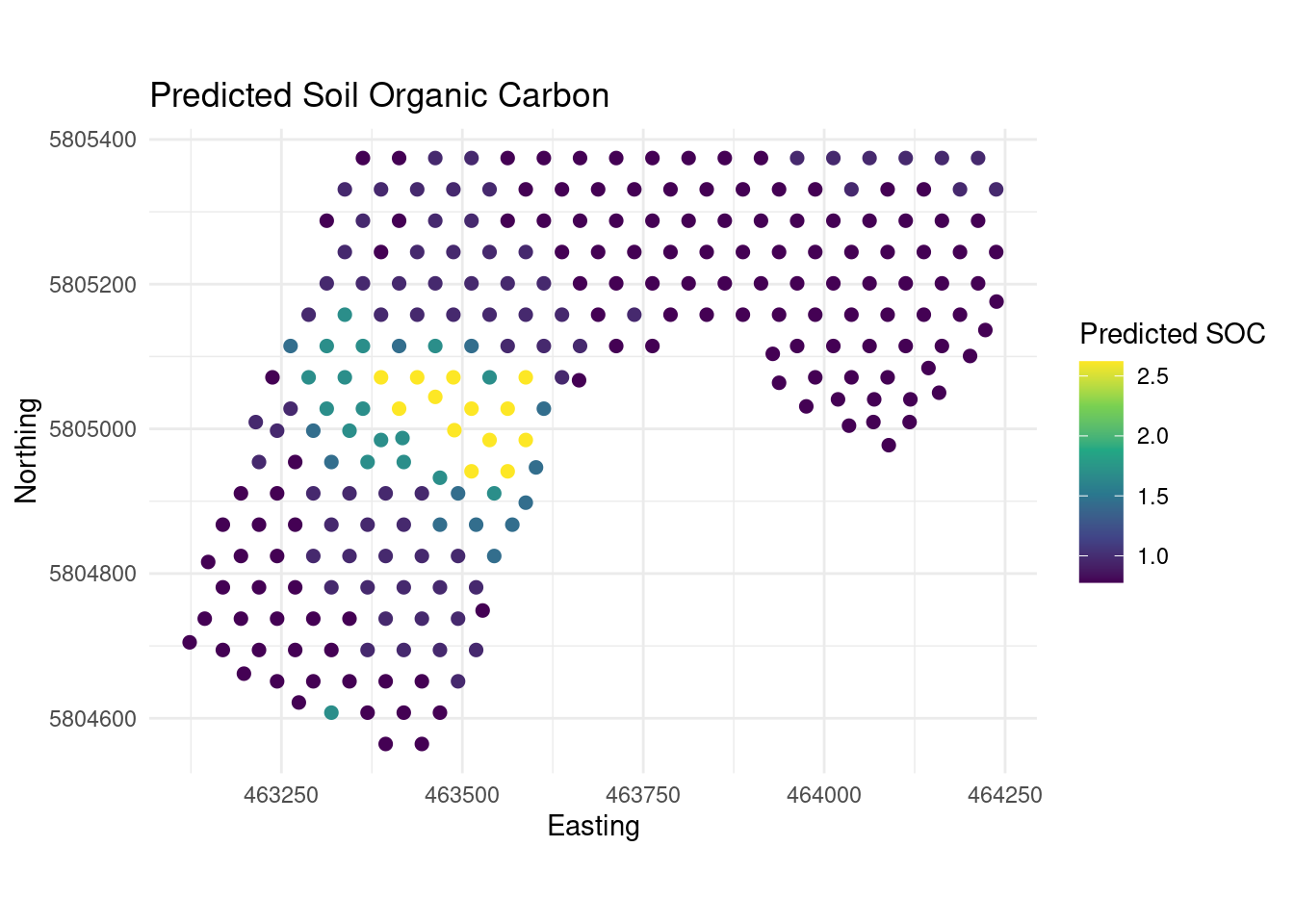
BB.250$SOC_pred <- predict(rtree_soc_model, newdata = BB.250)

20.4.6.2 Calculate residuals

BB.250$SOC_resid <- BB.250$SOC_target - BB.250$SOC_pred

20.4.6.3 Plots

20.4.7 Model performance

20.4.7.1 Plot residuals vs predicted values

plot(BB.250$SOC_pred, BB.250$SOC_resid,
     xlab = "Predicted SOC", ylab = "Residuals",
     main = "Residuals vs Predicted SOC")
abline(h = 0, lty = 2, col = "gray")

20.4.7.2 Compute RMSE

library(Metrics)
rmse(BB.250$SOC_target, BB.250$SOC_pred)
#> [1] 0.1884712

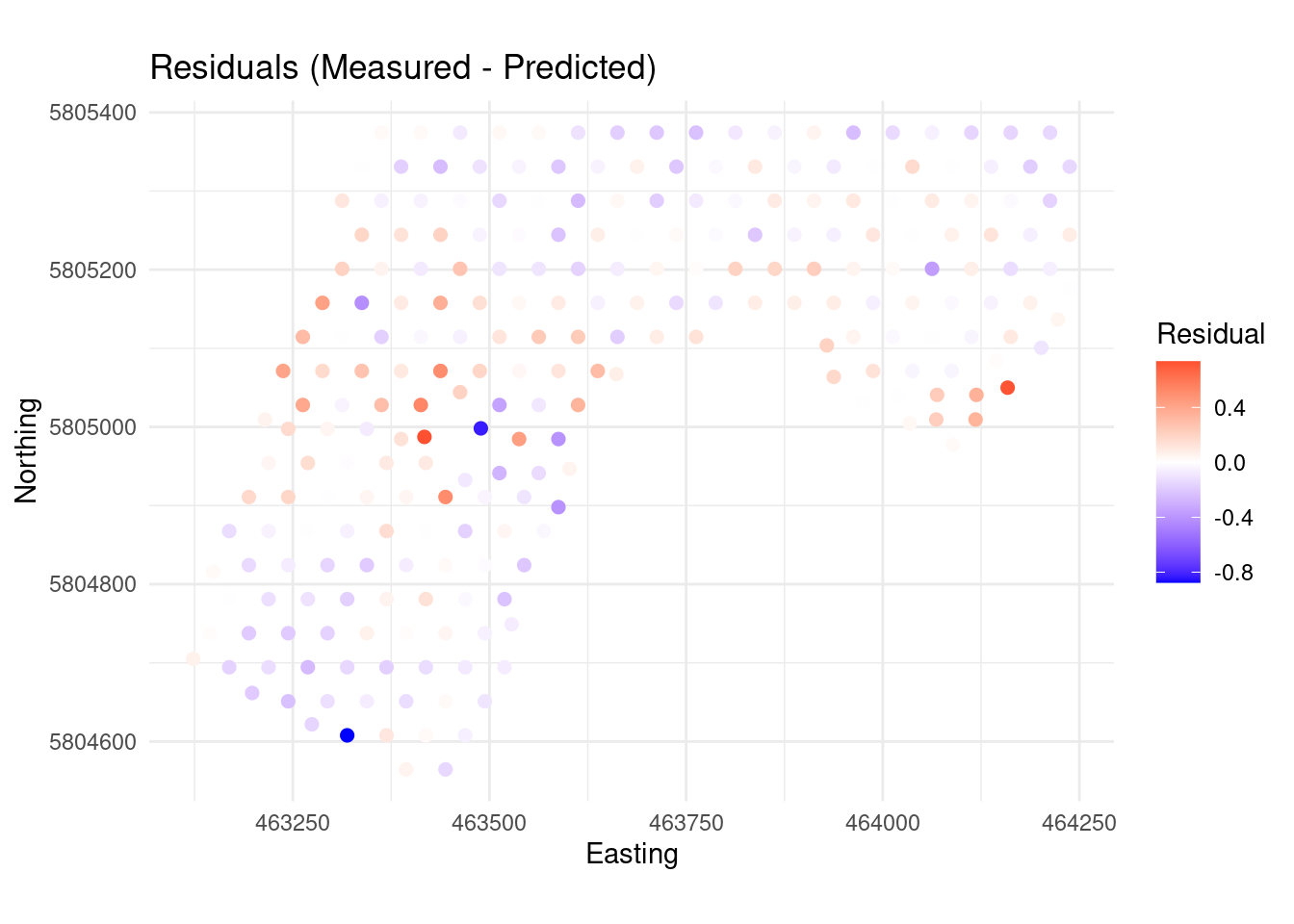
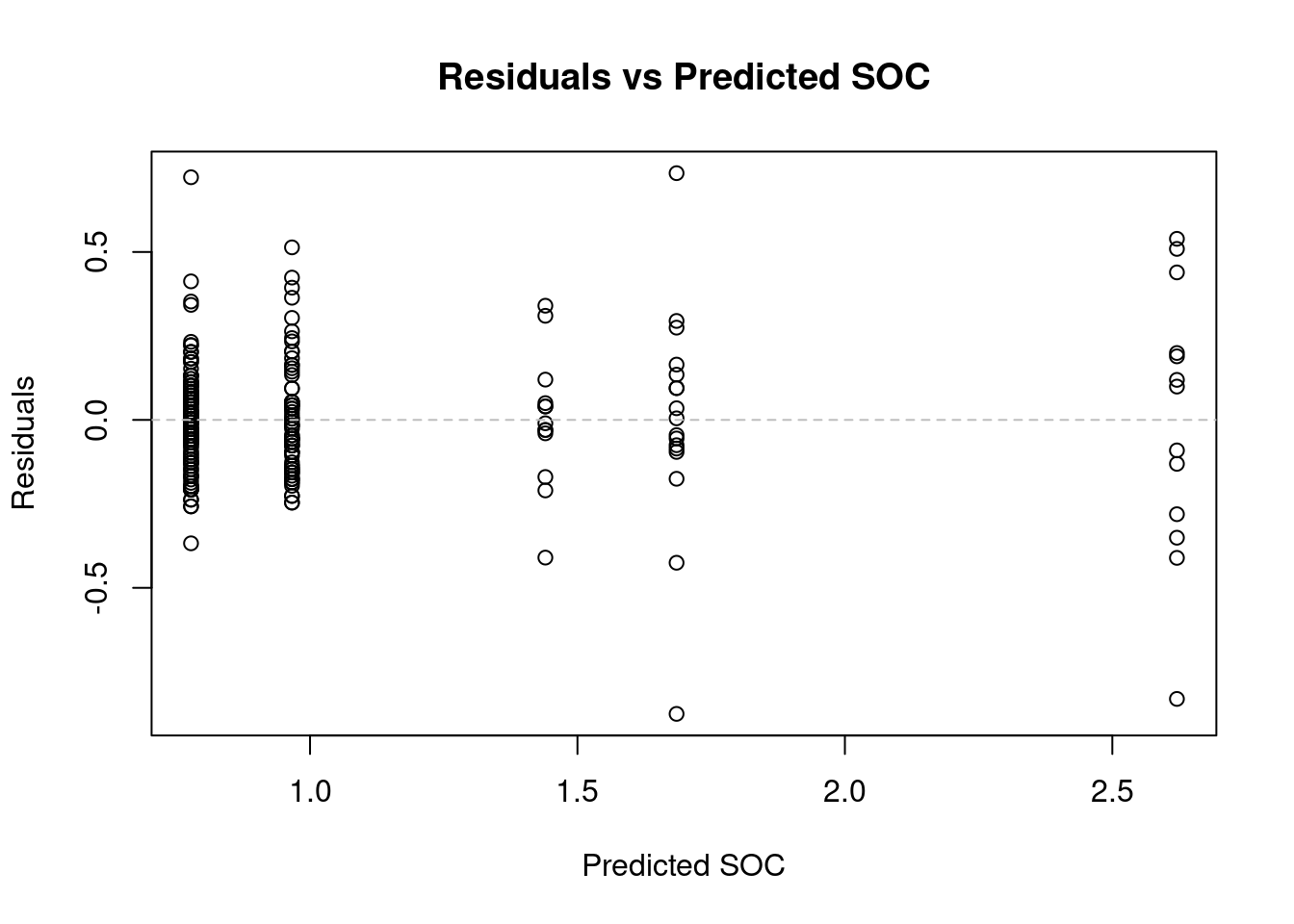
20.4.8 In summary

Each split makes the model more precise, dividing the data into smaller and more homogeneous groups.
The final prediction for a location is simply the average SOC of the group (leaf) where it ends up.
The tree helps us understand how SOC varies based on measurable factors like ERa or NDVI.

This makes regression trees very useful not only for prediction, but also for interpreting which variables matter, and how they interact in real-world data.

20.5 Model validation

Once a regression tree is fitted, it is essential to evaluate how well it performs on unseen data. This allows us to estimate its ability to generalize — that is, to make accurate predictions at locations or times that were not used to train the model.

20.5.1 Cross-validation

Cross-validation (CV) is a common and effective way to assess model performance. Instead of relying on a single split between training and validation data, CV systematically partitions the data into subsets (called folds) and rotates them through training and validation roles.

See the section Spatial Cross-Validation.

20.5.2 Performance metrics

The most common metrics to assess regression performance are:

RMSE (Root Mean Squared Error): penalizes large errors and is sensitive to outliers.
MAE (Mean Absolute Error): provides a more robust measure of average error magnitude.

They can be computed as:

\[ \text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^n (z_i - \hat{z}i)^2 } \qquad \text{MAE} = \frac{1}{n} \sum{i=1}^n |z_i - \hat{z}_i| \]

where \(z_i\) is the observed value and \(\hat{z}_i\) is the predicted value for location i.

In R, these metrics can be calculated using the Metrics package or custom functions (as shown in previous chapters).

20.5.3 Comparing models

Once a performance measure is defined, it becomes possible to compare the regression tree to other models:

Null model: predicts the global average (baseline).
Linear regression: models the target as a linear combination of covariates.
Other interpolators: e.g., nearest neighbour(s), IDW, kriging.

A table summarizing RMSE or MAE values across models can guide model selection.

20.6 Extension to the spatial context

Regression trees are not inherently spatial models. They do not exploit the geographic location of observations unless it is explicitly included as a predictor. Therefore, when applied to spatial data, a regression tree behaves as a “stepwise interpolator” — creating sharp boundaries in space where predictions change abruptly from one region to another.

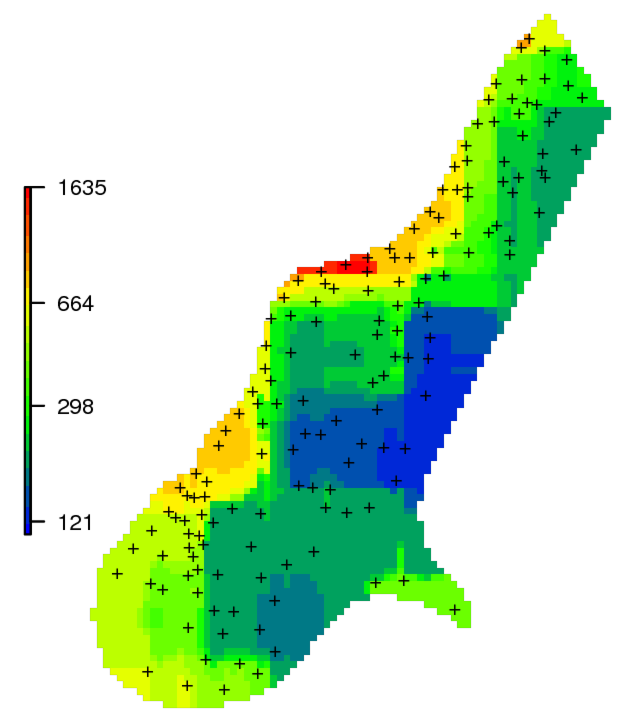
Zinc concentration map from the Meuse dataset illustrating sharp transitions typical of regression tree-based spatial predictions.

Figure 20.3: Zinc concentration map from the Meuse dataset illustrating sharp transitions typical of regression tree-based spatial predictions.

This leads to predictions that are not spatially continuous, unlike geostatistical methods (e.g. kriging), which produce smooth surfaces and account for spatial autocorrelation.

20.6.1 Strengths and limitations in spatial settings

Using regression trees in spatial applications has both advantages and drawbacks:

Table 20.2: Table 20.3: Strengths and Limitations of Regression Trees in Spatial Contexts
Strengths	Limitations
Can handle complex, non-linear relationships	No spatial continuity in predictions
Works well with many predictors, including categorical ones	Does not account for spatial autocorrelation
Robust to outliers and missing data	Can create unrealistic step boundaries in space
Interpretable and easy to visualize	Sensitive to overfitting if not pruned

In many environmental and ecological applications, spatial structure matters — variables measured at nearby locations tend to be similar (spatial autocorrelation). Ignoring this may reduce prediction accuracy or generate artifacts in mapped outputs.

20.6.2 Making trees spatially aware: possible strategies

Several strategies can be used to adapt regression trees for spatial prediction.

20.6.2.1 Use coordinates as predictors

The simplest way to introduce spatial awareness is to include X and Y coordinates as explanatory variables:

SOC_target ~ x_25833 + y_25833 + NDVI + ERa + …

This allows the tree to “learn” spatial patterns — for example, to create splits based on longitude or latitude ranges — but it is still limited. The tree learns spatial structure indirectly and may overfit specific locations without modeling smooth transitions.

20.6.2.2 Residual kriging

A more rigorous approach is to combine regression trees with geostatistics. The idea is to:

Fit a regression tree to model the deterministic trend.
Compute the residuals between observed and predicted values.
Apply kriging to interpolate the residuals based on spatial autocorrelation.
Add the kriged residuals back to the tree predictions.

This hybrid method — often called regression kriging — combines the flexibility of machine learning with the smoothness and spatial coherence of geostatistics.

20.6.2.3 Random Forest and ensembles

Random forest is an ensemble method that builds many regression trees and averages their predictions. It generally improves accuracy and reduces overfitting. While still not explicitly spatial, a random forest can better capture complex spatial patterns when coordinates and spatial covariates are included.

In practice, random forests can be paired with residual kriging in the same way as single trees, creating a powerful spatial prediction framework.

See the section Random Forests for more details.

19 Kriging

21 Random Forests