14 Proximity Polygons
Proximity polygons can be also called Thiessen polygons or Voronoi polygons or nearest neighbour (i.e. one nearest neighbour).
14.1 Voronoi diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects.
It can be classified also as a tessellation.
For each point there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that point than to any other.
(See Wiki > Voronoi diagram)
thie_pol <- st_voronoi( st_union(n) )
plot(neigh$geometry,col='gray',reset=FALSE)
plot(thie_pol,col=NA,add=TRUE)
plot(n,add=TRUE,pch=16,col='black',cex=0.8)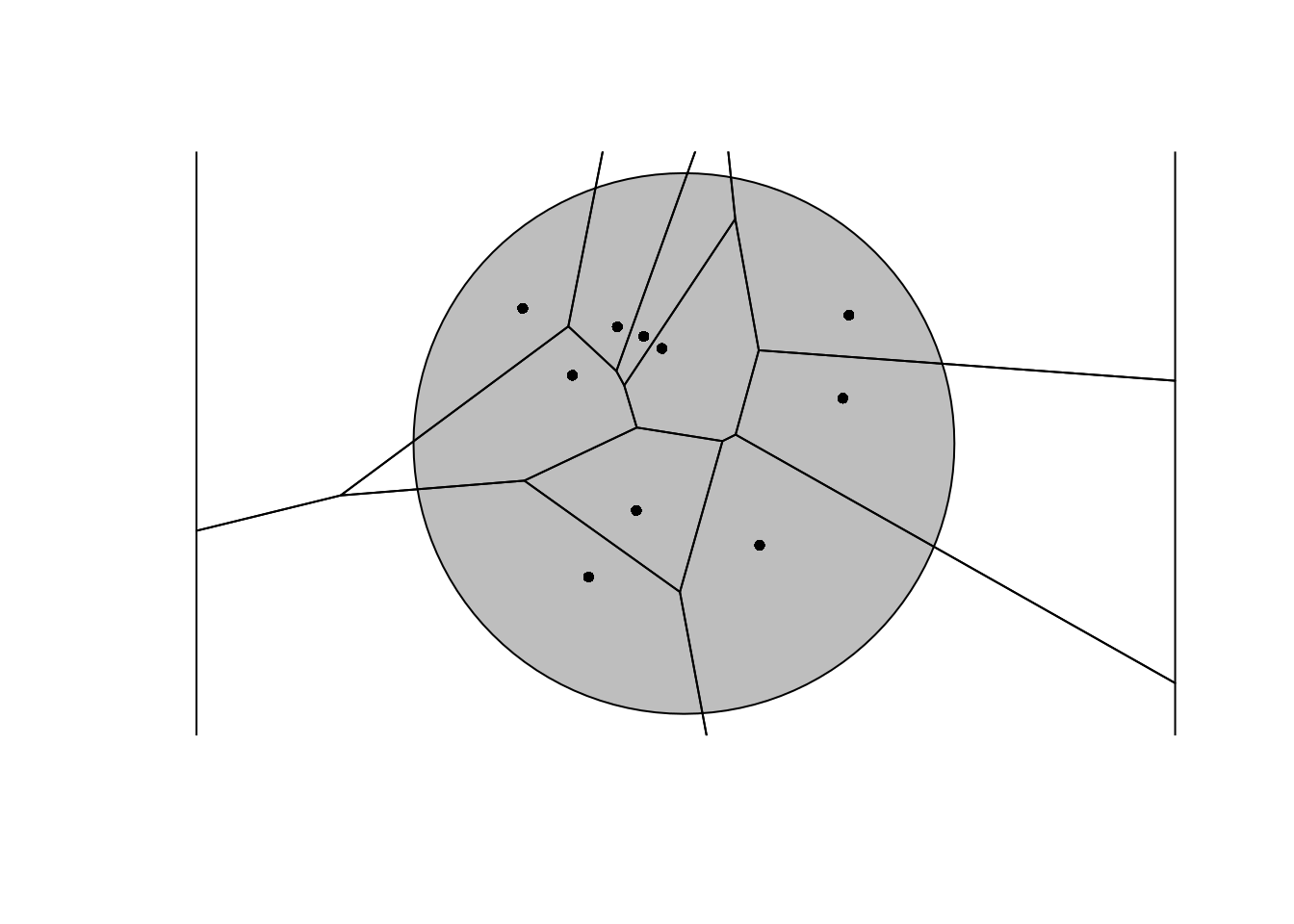
14.2 Nearest Neighbour interpolation
In this section the nearest neighbour interpolation is carried out using the set of point locations shown before. Nearest neighbour can be also used to interpolate categorical variables, but in the following example continuous quantitative variables are used.
NOTE: Please, check that the value interpolated at \(({\mathbf u})\) (red point) is the nearest neighbour interpolation using the closest observation (green point).
14.2.1 Demonstrate the usefulness of the Voronoi diagram
The Voronoi diagram clearly shows that the unknown red point \(({\mathbf u})\) belongs to the Voronoi cell of the green point, which is the closest observation point as highlighted also in the previous plot.
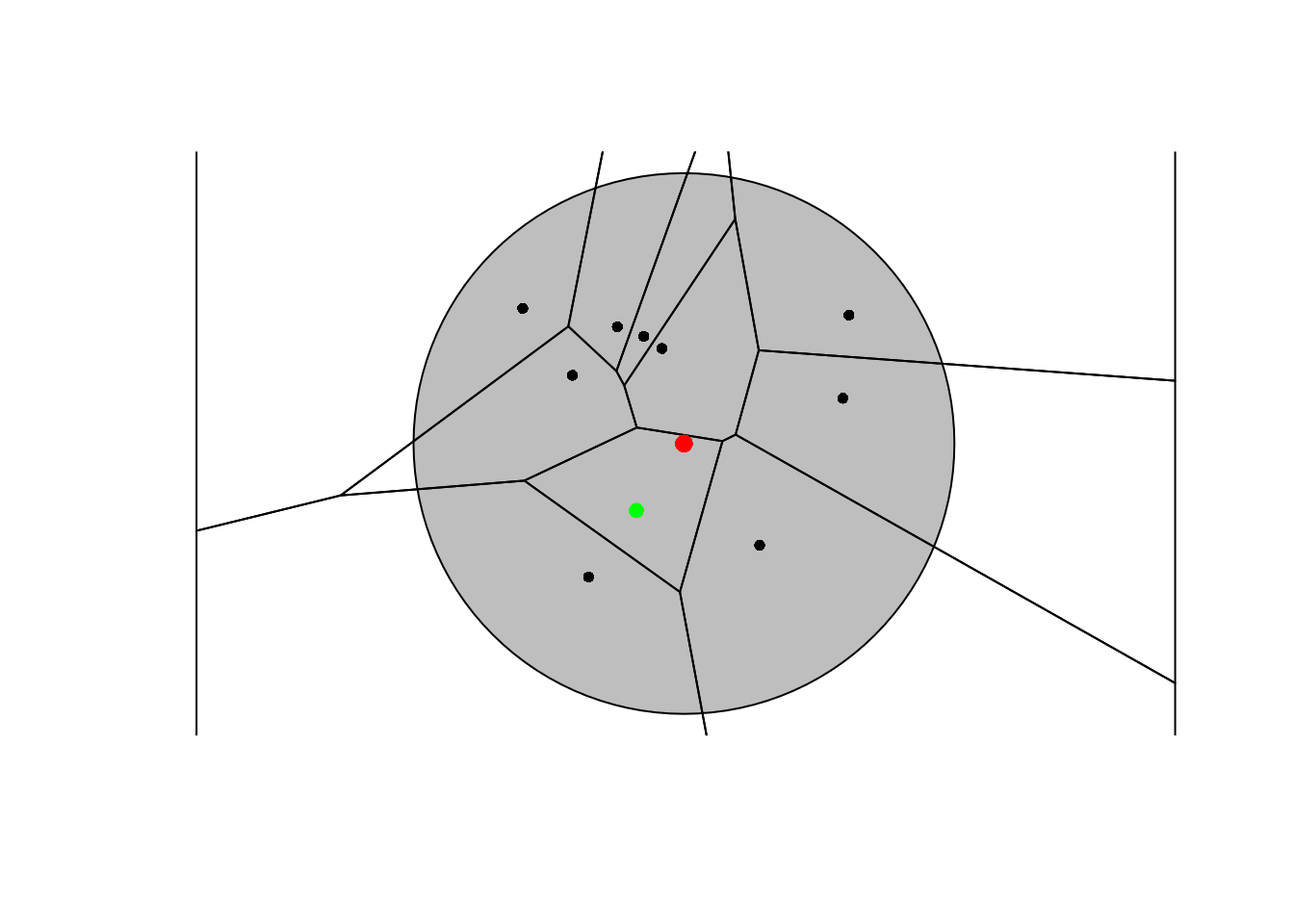
14.2.2 Interpolation
Given a generic unknown location \(({\mathbf u})\) as in the figure above, the formula is the following:
\(\hat{z}({\mathbf u}) = \displaystyle\sum_{\alpha=1}^{n({\mathbf u})} \lambda_{\alpha}({\mathbf u}) z({\mathbf u}_{\alpha})\)
Weights must sum up to one:
\(\sum_{\alpha=1}^{n({\mathbf u})} \lambda_{\alpha}({\mathbf u}) = 1\)
The nearest neighbor interpolation is conducted by assigning a weight, \(\lambda_{1}({\mathbf u})=1\), to the observation location that is closest to the unknown location \(({\mathbf u})\). All other observation locations are assigned a weight \(\lambda_{\alpha}({\mathbf u})=0\,,\;\; \forall\, \alpha=2,...,n({\mathbf u})\).