11 Understanding Spatial Variability

11.1 Understanding Random Fields and Their Statistical Distribution

A random field is a function that assigns a random variable to every location in space. In the spatial context, we can think of a random field as a map of values, each of which is the outcome of a random process occurring at a specific location.

Formally, a random field $Z(\mathbf{s})$ is defined over a domain $\mathbf{s} \in D \subset \mathbb{R}^2$, where each location $\mathbf{s} = (x, y)$ has a corresponding random variable.

$A random field $Z(\mathbf{s})$ defined over a spatial domain $D \subset \mathbb{R}^2$. Each black point represents a spatial location $\mathbf{s}_i$, to which a random variable $Z(\mathbf{s}_i)$ is associated. Selected locations display their probability distribution, illustrating that the field is composed of spatially indexed random variables.$

Figure 11.1: A random field $Z(\mathbf{s})$ defined over a spatial domain $D \subset \mathbb{R}^2$. Each black point represents a spatial location $\mathbf{s}_i$, to which a random variable $Z(\mathbf{s}_i)$ is associated. Selected locations display their probability distribution, illustrating that the field is composed of spatially indexed random variables.

Didactic notes on the figure:

The use of a regular grid with black dots effectively represents a discrete spatial domain over which a spatial process is defined.
The vertically emerging bell-shaped curves emphasize that each location $\mathbf{s}_i$ is associated with a random variable $Z(\mathbf{s}_i)$, governed by a probability distribution.
The notation $Z(\mathbf{s})$ refers to the random field as a whole — a spatial function mapping each location to a random variable — while $Z(\mathbf{s}_i)$ denotes the random variable at a specific point.
Only a subset of these random variables is explicitly visualized, reinforcing that the field is defined over the entire domain, not just the displayed points.
The coordinate notation is $\mathbf{s}_1 = (x_1, y_1)$, which clarifies that each location belongs to the spatial domain $D \subset \mathbb{R}^2$.
At location $\mathbf{s}_1$, the figure highlights the probabilistic selection of a specific value from the bell-shaped curve (gaussian distribution) using a dashed line. This single outcome, $z(\mathbf{s}_1)$, is called a regionalized value — the observed value of the random variable $Z(\mathbf{s}_1)$ at that location.
Extending this idea to all locations in the spatial domain, the set of regionalized values $\{z(\mathbf{s}_i)\}$ forms a regionalized variable $z(\mathbf{s})$. It represents a spatially continuous (or discrete) field of observed values (observed field) that stems from a single realization of the underlying random field $Z(\mathbf{s})$.
Each bell-shaped curve represents the full probability distribution of the random variable $Z(\mathbf{s}_i)$, not just a single value. While we observe only one outcome (the regionalized value), conceptually, many realizations are possible — and their average would converge to the mean of the distribution.

We typically assume that the field is second-order stationary, meaning that:

The mean is constant across space: \[ \mathbb{E}[Z(\mathbf{s})] = \mu, \quad \forall\; \mathbf{s} \]
The variance is constant: \[ \text{Var}(Z(\mathbf{s})) = \sigma^2, \ \forall\; \mathbf{s} \]
The covariance between any two locations depends only on the separation vector $h = \|\mathbf{s}_1 - \mathbf{s}_2\|$ (and not on the absolute position): \[ \text{Cov}(Z(\mathbf{s}_1), Z(\mathbf{s}_2)) = C(\mathbf{h}), \ \text{where} \ \mathbf{h} = \mathbf{s}_1 - \mathbf{s}_2 \]

And if you further assume isotropy, then: \[ C(\mathbf{h}) = C(\|\mathbf{h}\|) \] i.e. the covariance depends only on the distance, not the direction.

When modeling such fields, we often assume that the random variables follow a Gaussian distribution. This implies that the entire field $Z$ is a realization of a multivariate normal distribution:

\[ Z \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{C}) \]

where:

$\boldsymbol{\mu}$ is the mean vector (often constant),
$\mathbf{C}$ is the covariance matrix derived from the spatial covariance function (e.g., exponential, spherical).

A particularly important case is the white noise field, where the random variables are independent and identically distributed (i.i.d.):

\[ Z(\mathbf{s}) \overset{\text{i.i.d.}}{\sim} \mathcal{N}(0, \sigma^2) \]

In this case, the covariance matrix $\mathbf{C}$ reduces to a diagonal matrix — and no spatial structure is present.

Later, we will introduce spatially correlated random fields, where nearby values are similar due to a structured covariance. These spatial dependencies give rise to rich patterns that we can simulate and analyze.

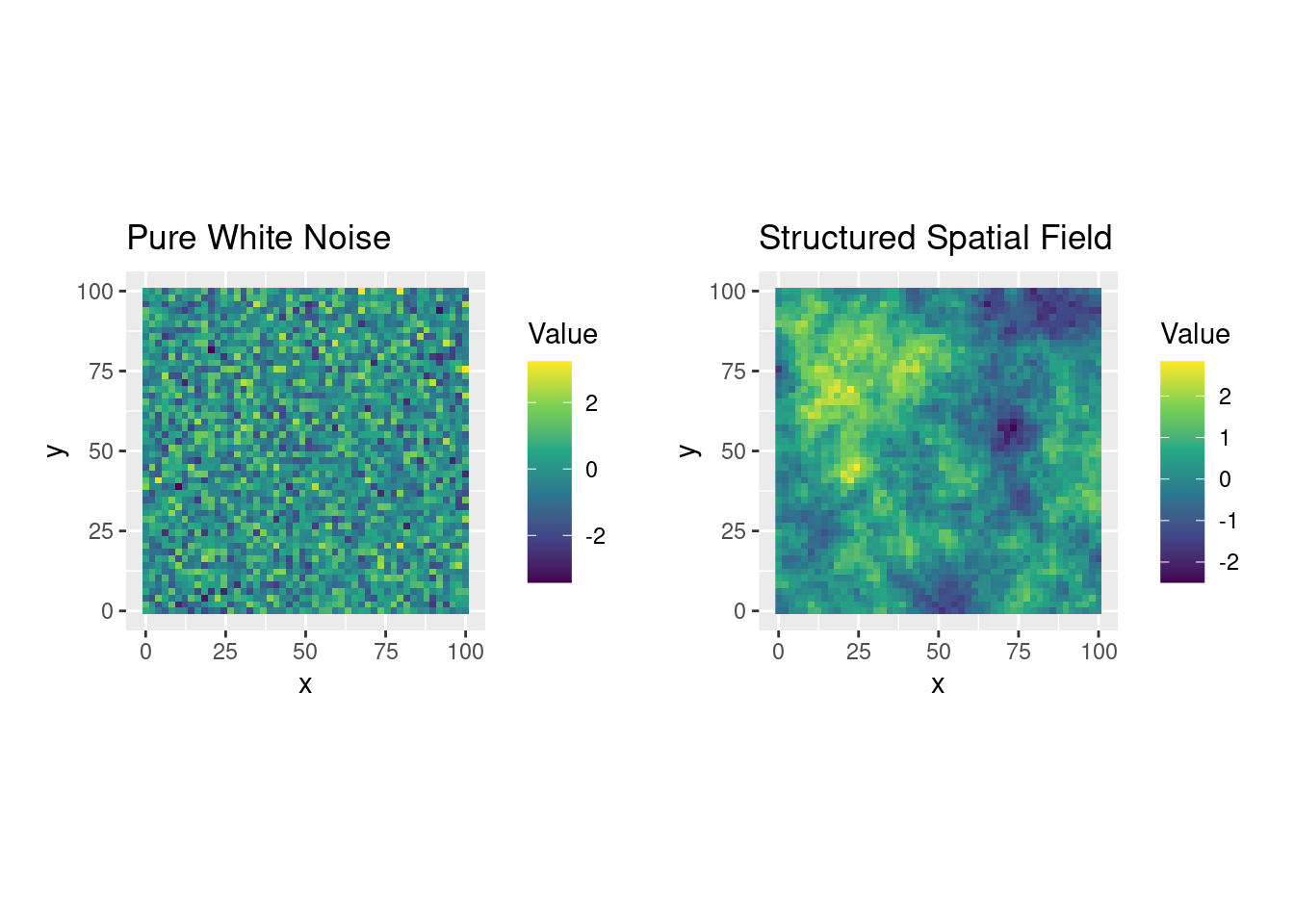
Figure 11.2: Two random fields: one with no spatial structure (left) and one with evident spatial correlation (right).

11.2 Introducing Spatial Correlation

In a purely random field, the value at each location is independent of its neighbors. However, many natural processes — including soil properties, elevation, or temperature — tend to vary gradually in space, meaning that nearby values are more similar than distant ones (Tobler’s Law). This phenomenon is called spatial autocorrelation.

11.2.1 Spatial Covariance Matrix

To represent spatial correlation mathematically, we use a covariance matrix $\mathbf{C}$, where each element $C_{ij}$ describes how strongly the value at location $\mathbf{s}_i$ is correlated with the value at location $\mathbf{s}_j$.

For a stationary and isotropic process, the covariance depends only on the distance $h = \|\mathbf{s}_i - \mathbf{s}_j\|$, not on the absolute position or direction. That is:

\[ C_{ij} = C(h) = \text{Cov}(Z(\mathbf{s}_i), Z(\mathbf{s}_j)) = \sigma^2 \cdot \rho(h) \]

where:

$\sigma^2$ is the variance of the process (also called the sill),
$\rho(h)$ is the correlation function (e.g., exponential, spherical), which decays with distance.

Note:
Given two observed values of a variable at spatial locations $\mathbf{s}_1$ and $\mathbf{s}_2$,
say $Z(\mathbf{s}_1) = 0.12$ and $Z(\mathbf{s}_2) = 0.10$, and the mean $\bar{Z} = 0.11$,
the sample covariance is:

\[ \text{Cov}(Z(\mathbf{s}_1), Z(\mathbf{s}_2)) = (0.12 - 0.11)(0.10 - 0.11) = -0.001 \]

A common choice is the exponential model:

\[ \rho(h) = \exp\left(-\frac{h}{r}\right) \]

Here, $r$ is the range parameter, which determines how quickly correlation drops with distance. For instance, if $h = r$, then the correlation between two points is $\approx 0.37$.

11.2.2 Simulating Spatial Fields from a Covariance Matrix

To simulate a spatial field with this correlation structure, we follow these steps:

Build the covariance matrix $\mathbf{C}$ using the chosen correlation function
Decompose the matrix using Cholesky decomposition: \[ \mathbf{C} = \mathbf{L} \mathbf{L}^\top \]
Generate a vector of independent Gaussian noise: \[ \mathbf{G} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \]
Multiply to create a spatially correlated field: \[ \mathbf{Z} = \mathbf{L} \cdot \mathbf{G} \]

The result is a realization of a Gaussian random field with spatial correlation. Visually, the field appears smooth, with values transitioning gradually over space.

11.2.3 Comparison

Property	Pure Random Field	Spatially Correlated Field
Covariance Matrix	Diagonal (no correlation)	Full matrix (distance-dependent)
Visual Appearance	Grainy, noisy	Smooth, continuous patterns
Mathematical Structure	$\mathbf{Z} \sim \mathcal{N}(\mathbf{0}, \sigma^2 \mathbf{I})$	$\mathbf{Z} \sim \mathcal{N}(\mathbf{0}, \mathbf{C})$

11.3 Simulating Spatial Fields: From Theory to Practice

Briefly recap the idea that we can now generate fields with and without structure.
Introduce the simulation approach using covariance functions and Cholesky decomposition.
Include the actual simulation plots (as you already created).
Highlight how changing the range or sill alters the visual structure.

To better understand how spatial correlation shapes the structure of a random field, we can simulate artificial spatial data with and without correlation. This hands-on approach helps reveal how theory translates into visible spatial patterns.

We use a Gaussian random field model, where the spatial dependence is encoded through a covariance matrix $\mathbf{C}$. By applying the Cholesky decomposition, we can generate realizations that follow this prescribed structure.

11.3.1 Step-by-Step Procedure

Define a grid of spatial locations $\mathbf{s}_1, \mathbf{s}_2, \ldots, \mathbf{s}_n$.

# Grid definition
n <- 50
grid <- expand.grid(x = seq(0, 100, length.out = n),
                    y = seq(0, 100, length.out = n))

Compute all pairwise distances to form a distance matrix.

coords <- as.matrix(grid)
dist_matrix <- as.matrix(dist(coords))

Build the covariance matrix $\mathbf{C}$ using a chosen correlation model, such as the exponential: \[ C(h) = \sigma^2 \cdot \exp\left( -\frac{h}{r} \right) \] where:
- $\sigma^2$ is the variance (sill),
- $r$ is the range,
- $h$ is the distance between two locations.

# Covariance function
cov_function <- function(sill, range, h) {
  sill * exp(-h / range)
}

Apply the Cholesky decomposition: \[ \mathbf{C} = \mathbf{L} \mathbf{L}^\top \] where $\mathbf{L}$ is a lower triangular matrix.

# Structured field: covariance matrix and Cholesky
sill <- 1
range <- 20
C <- cov_function(sill, range, h = dist_matrix)
L <- chol(C)

Generate independent standard normal values: \[ \mathbf{G} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \]

set.seed(234)
G <- rnorm(nrow(grid), 0, 1)

Construct the correlated field: \[ \mathbf{Z} = \mathbf{L} \cdot \mathbf{G} \]

z_structured <- crossprod(L, G)

Generate the uncorrelated field with matching variance:
This field is composed of independent values drawn from a normal distribution with the same variance as the correlated field (i.e., the sill), allowing for a fair comparison. \[ \mathbf{Z}_\text{random} \sim \mathcal{N}(0, \sigma^2), \quad \text{with } \sigma^2 = \text{sill} \]

# Random field: pure nugget with same variance as structured field
set.seed(678)
z_random <- rnorm(nrow(grid), 0, sqrt(sill))

This vector $\mathbf{Z}$ represents a realization of a spatially correlated process. We can compare it to a white noise field (no spatial correlation), where each location receives a value drawn independently from the same normal distribution.

11.3.2 Visual Example

Below are two simulated spatial fields over the same grid:

Left: a pure white noise field (no spatial correlation)
Right: a structured field with exponential spatial correlation

library(ggplot2)
library(patchwork)
library(viridis)
library(gridExtra)

# Prepare data for plotting
df <- grid
df$structured <- as.numeric(z_structured)
df$random <- z_random

# Plot
p1 <- ggplot(df, aes(x, y, fill = random)) +
  geom_raster() +
  coord_equal() +
  scale_fill_viridis_c() +
  labs(title = "Pure White Noise", fill = "Value")

p2 <- ggplot(df, aes(x, y, fill = structured)) +
  geom_raster() +
  coord_equal() +
  scale_fill_viridis_c() +
  labs(title = "Spatially Correlated Field", fill = "Value")

grid.arrange(p1, p2, ncol = 2)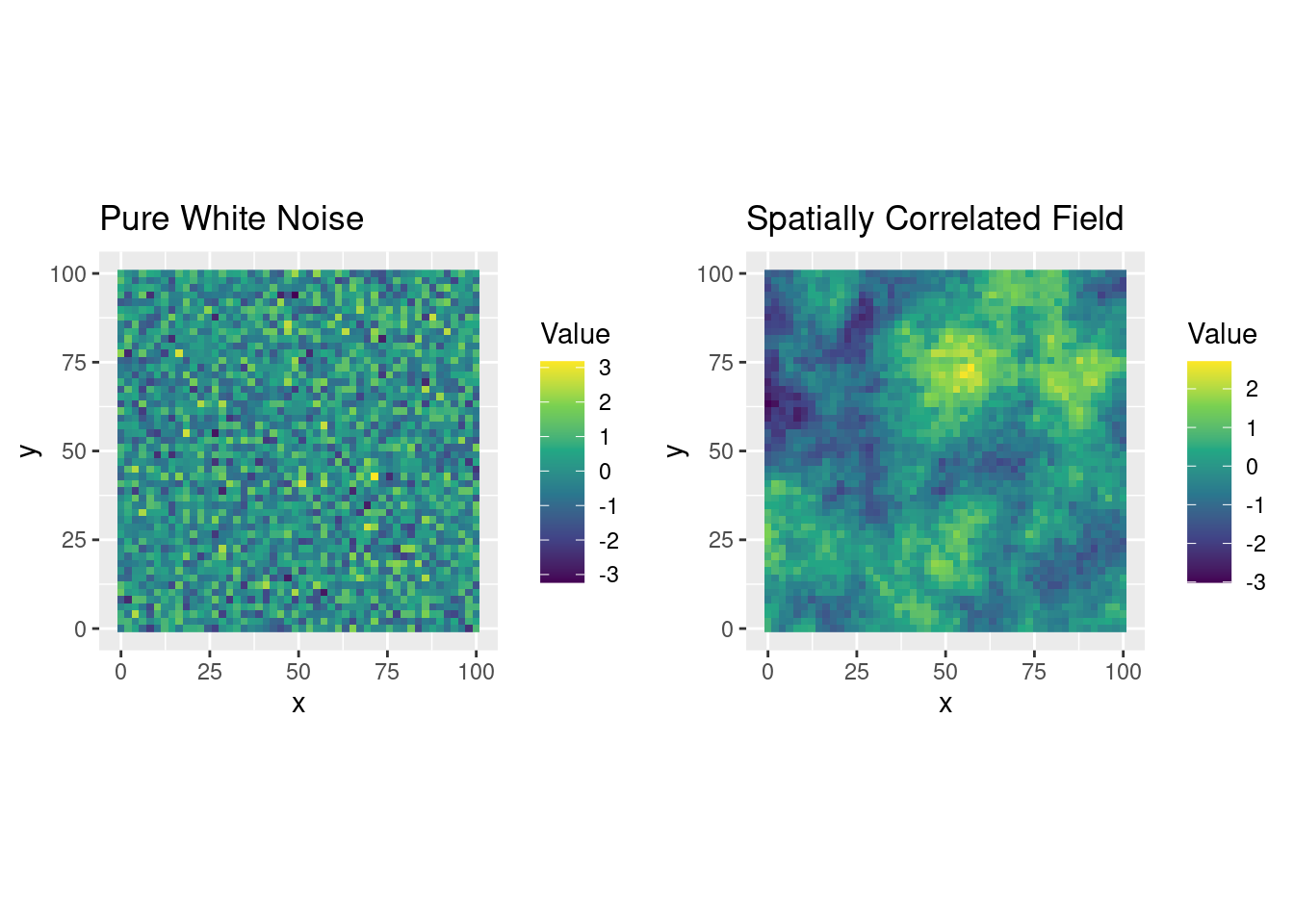

Figure 11.3: Comparison between white noise and a spatially structured random field

As we can see, the spatially structured field exhibits continuity, with values changing gradually over space, unlike the grainy appearance of white noise.

This experiment shows how a well-defined covariance model creates smoothness, and how the range parameter controls the scale of spatial dependence.

11.4 Decomposing a Spatial Field into Components

Introduce the conceptual idea of trend + structure + noise
Define:
$\mu(\mathbf{s})$: deterministic trend
$S(\mathbf{s})$: spatially correlated residual
$\varepsilon(\mathbf{s})$: nugget or white noisez
Relate this to physical/geographical phenomena (e.g., SOC increases with altitude but with local variability).

In many real-world applications, a spatial variable is not entirely random. Its spatial variability can often be explained as the sum of three conceptually distinct components:

\[Z(\mathbf{s}) = \mu(\mathbf{s}) + S(\mathbf{s}) + \varepsilon(\mathbf{s})\] where:

$\mu(\mathbf{s})$ is the trend component, often driven by known environmental covariates (e.g., coordinates, elevation);
$S(\mathbf{s})$ is the structured residual, accounting for spatial autocorrelation not explained by the trend;
$\varepsilon(\mathbf{s})$ is a spatial white noise term, including the nugget effect, i.e., micro-scale variation and measurement noise.

This decomposition is central in geostatistics and spatial modeling because each component has a different origin and must be handled accordingly.

Before delving into the mathematical details of each component of a spatial random field, an illustrative example is here provided. The figure below shows the simulated decomposition of a spatial field into:

a deterministic trend depending on spatial coordinates and elevation,
a short-range spatial structure capturing local continuity,
a long-range spatial structure capturing broad-scale variation,
a spatial white noise component is often introduced in simulations to represent local variability that is uncorrelated in space. While part of this unstructured variation may correspond to the nugget effect — such as measurement error or unresolved micro-scale variation — it can also include other forms of high-frequency noise that are not captured by the structured spatial model.

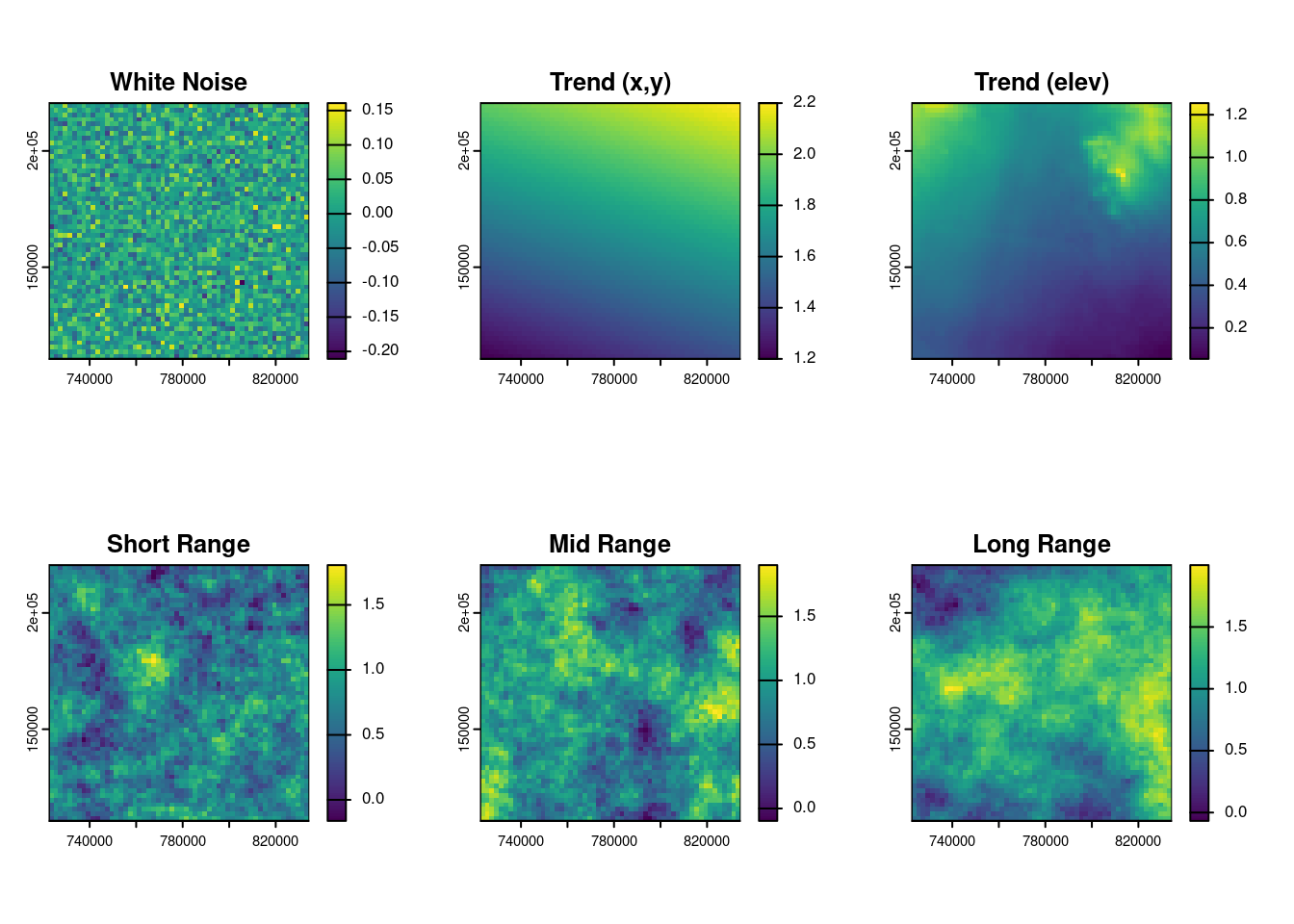
Figure 11.4: Compponents of the spatial field.

The final simulated field is obtained as the sum of these components. This visual decomposition helps build intuition on how spatial variability arises from both structured and unstructured sources.

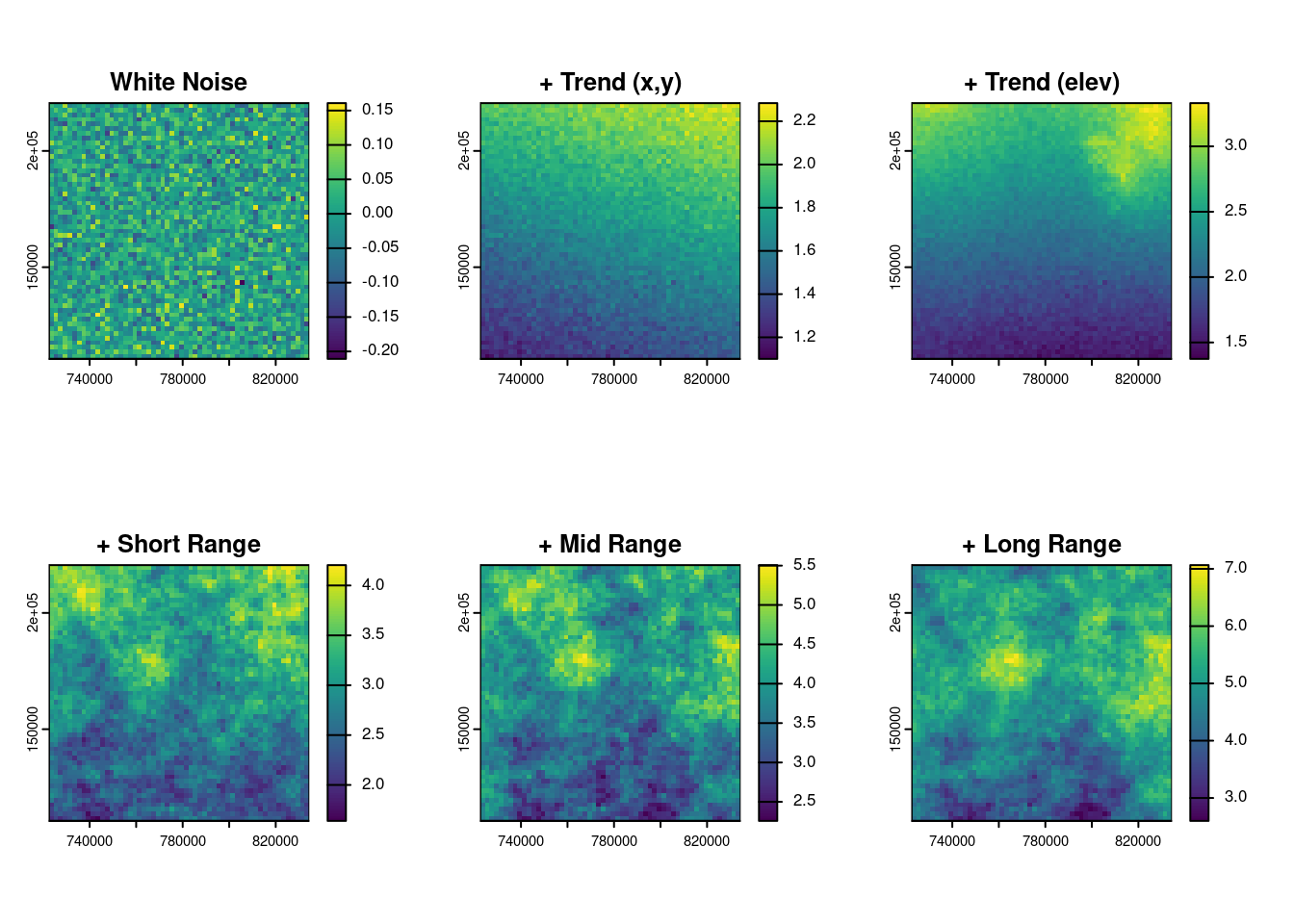
Figure 11.5: From noise to structure: the relative contribution of spatial components.

11.4.1 Trend Component: Large-Scale Variation

The trend represents the deterministic part of the spatial field. It captures gradual, systematic changes over space and may depend on covariates such as elevation or location:

\[ \mu(\mathbf{s}) = \beta_0 + \beta_1 x + \beta_2 y + \beta_3 z \] This component explains long-range variation — for instance, an increasing soil property with altitude or a west-to-east gradient.

11.4.2 Structured Residual: Spatial Dependence

The residual component $S(\mathbf{s})$ represents the spatially correlated part of the variation that is not explained by the trend. It captures medium- to short-range dependence, such as clusters of similar values.

This component is modeled via a covariance function and often simulated using Cholesky decomposition, as shown earlier.

11.4.3 Nugget Effect: Random Noise

The nugget $\varepsilon(\mathbf{s})$ models purely uncorrelated random noise. It may reflect measurement error or spatial variability occurring at scales finer than our sampling resolution.

Visually, this component introduces local “graininess” into the spatial field.

11.4.4 Summary Table

Component	Description	Spatial Scale	Statistical Nature
$\mu(\mathbf{s})$	Deterministic trend (e.g. slope, elevation)	Long-range	Known function
$S(\mathbf{s})$	Structured residual	Medium/short-range	Random, correlated
$\varepsilon(\mathbf{s})$	Micro-scale variability or error	Very short-range	Random, uncorrelated

This decomposition enables a structured approach to modeling spatial variability, where each component is estimated, modeled, or simulated according to its nature.

11.5 Summary and Takeaways

Summarize what spatial variability means.
Reinforce the decomposition: trend + structure + nugget.
Mention that geostatistics builds on these ideas to estimate, interpolate, and model spatial processes.

11.6 Interactive Simulation of a Spatial Field

10 Regression

12 Digital (Soil) Mapping

Component	Description	Spatial Scale	Statistical Nature
\(\mu(\mathbf{s})\)	Deterministic trend (e.g. slope, elevation)	Long-range	Known function
\(S(\mathbf{s})\)	Structured residual	Medium/short-range	Random, correlated
\(\varepsilon(\mathbf{s})\)	Micro-scale variability or error	Very short-range	Random, uncorrelated